En la anterior entrada “El largo plazo: el riesgo disminuye, la rentabilidad no” se mostraba uno de los factores que ayuda a la reducción del riesgo de nuestra inversión: el largo plazo. Pero no es el único. En esta entrada veremos otro de los factores: la diversificación de nuestra cartera.
Con otro experimento, veremos hasta qué punto la diversificación influye en el riesgo de nuestra inversión.
El experimento es el siguiente. He escogido las 500 empresas del S&P500 y he calculado el comportamiento de 6 tipos de cartera en función del tamaño: carteras con una sola empresa, con 5, con 10, con 20, con 50, y finalmente con 100 empresas. El análisis lo he realizado para los últimos 5 años.
Por ejemplo, para la cartera con 10 empresas, vamos a estudiar el comportamiento de una cartera equiponderada al azar: esto es, escojo al azar 10 empresas de las 500 e invertimos en ellas en igual proporción. Y esto lo repito 100 veces para analizar qué efecto tiene sobre el riesgo las carteras de este tamaño.
Veamos lo que sale. En el siguiente gráfico se muestran las rentabilidades anuales obtenidas para cada tipo de cartera. Las líneas rojas de cada caja representan aproximadamente la rentabilidad media anual obtenida en cada tipo de cartera.
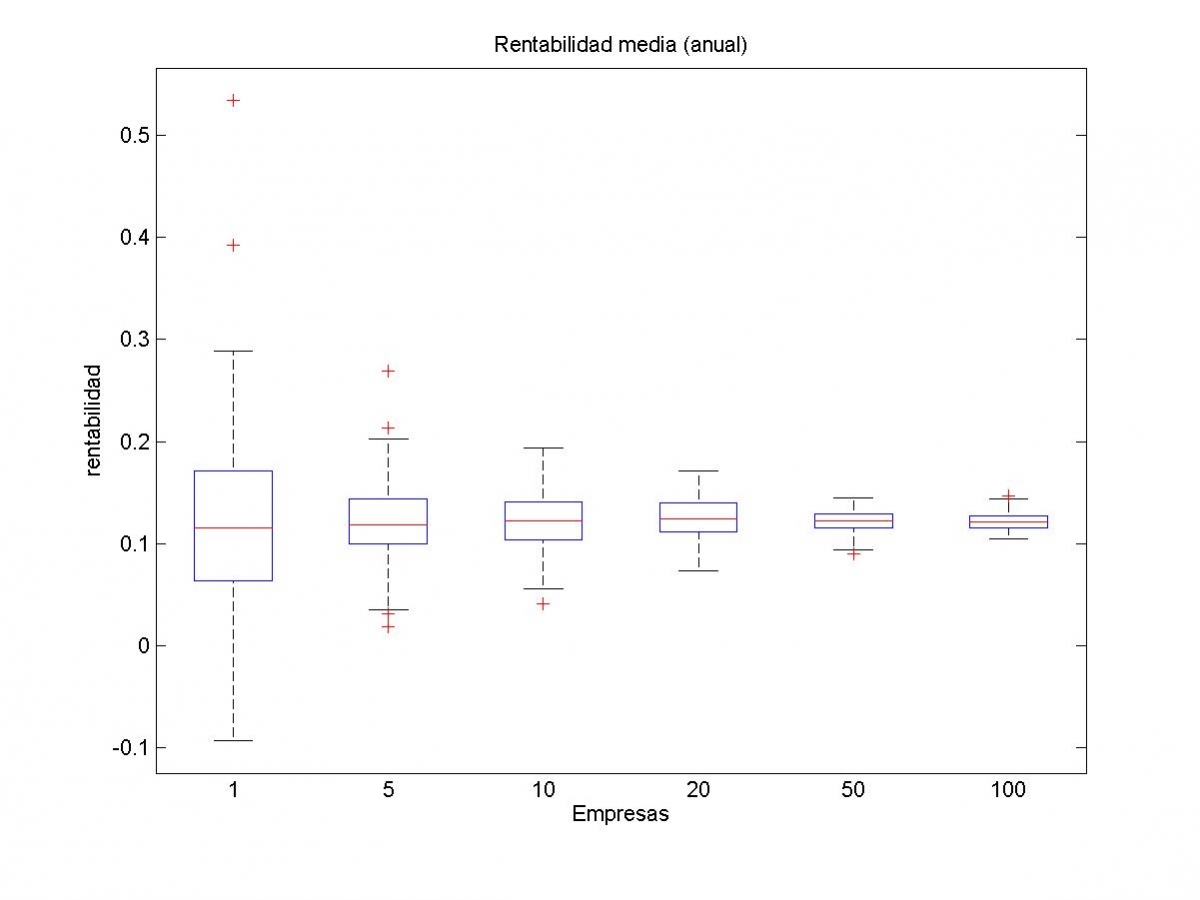
Se puede observar que, independientemente del tamaño de la cartera, la rentabilidad media anual es aproximadamente del 12% en todos los casos.
Sin embargo, el riesgo asumido es distinto en función del tamaño de la cartera. Por ejemplo, si en nuestra cartera solo tuviésemos una empresa, el 50% de las veces tendríamos una rentabilidad anual entre el 7% y el 17%. Si hubiésemos escogido muy bien la empresa de nuestra cartera (a priori prácticamente imposible), hubiésemos obtenido una rentabilidad media superior al 30%. Por el contrario, si hubiésemos escogido mal a esa empresa, la rentabilidad media hubiese sido del -10%. O sea, existe un riesgo considerable en carteras de una única empresa.
Pero según incrementamos el número de empresas de nuestra cartera, vemos que el riesgo anterior se reduce considerablemente y el comportamiento ya no depende de la elección de nuestras empresas. Por ejemplo, con una cartera de 100 empresas, e independientemente de cómo las hayamos elegido, la rentabilidad media es siempre mayor del 10% en todos los casos. Y la variabilidad es muy pequeña.
¿Pero hace falta una cartera tan grande para reducir el riesgo? Pues no necesariamente. Por ejemplo, con la cartera de 50 empresas vemos que el riesgo (amplitud de la caja) es muy parecido al de la cartera con 100 empresas. Aunque existe una probabilidad del 1% de elegir mal esas 50 empresas y obtengamos una rentabilidad algo inferior al 10%. Esta probabilidad, aunque pequeña, no se aprecia en las carteras de 100 empresas.
La razón de que no hace falta un gran número de empresas en la cartera se debe a que, según aumentamos el tamaño de la cartera, muchas de las empresas dependerán entre sí (tendrán correlaciones altas). Y las correlaciones altas no ayudan a reducir el riesgo. Podéis ver la entrada “Teoría Moderna de Carteras: un poco de Matemáticas” para entender mejor el concepto de correlación.
Esto quiere decir que si escogemos convenientemente bien 10 empresas (con baja correlación entre ellas) podríamos tener un riesgo menor que el de una cartera con 50 empresas.
El siguiente gráfico ilustra esta situación. Ahí se muestran los valores en riesgo (VaR) semanales al 95% para cada tipo de cartera. Si por ejemplo el VaR es del 10%, significa que con una probabilidad del 5% podemos llegar a perder más del 10% del dinero invertido. O sea, cuanto más grande peor.
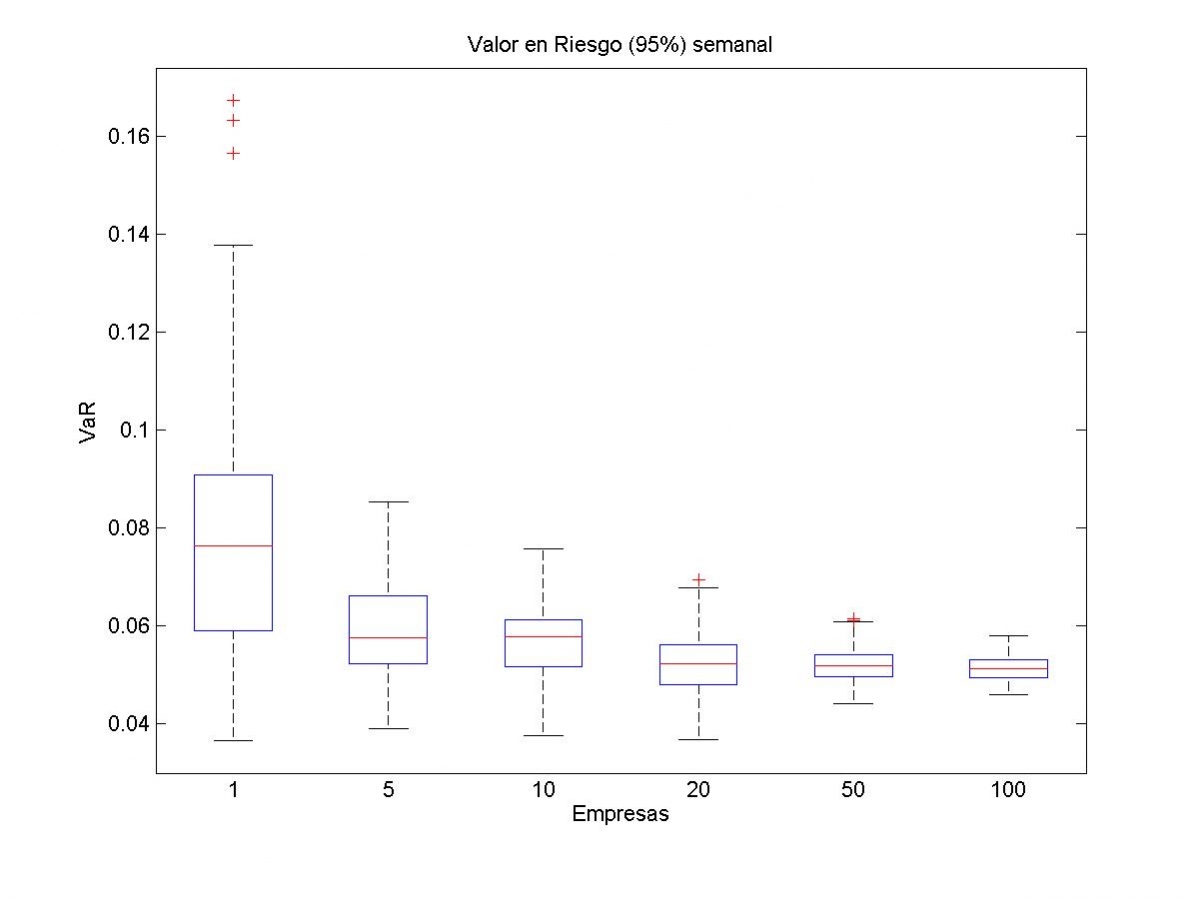
Se puede observar que con una sola empresa, la mayor parte de las veces la máxima pérdida semanal oscila bastante alrededor del 7.5%. En cambio, para una cartera de 100 empresas, la máxima pérdida semanal estaría muy centrada en el 5%, independientemente de cómo hayamos escogido esas 100 empresas.
Pero como decía antes, basta con escoger convenientemente 10 o 20 empresas para conseguir los mismos niveles de riesgo que una cartera de 100 empresas. Por ejemplo, en la caja de 10 empresas se observa que existen subconjuntos de 10 empresas con riesgos similares o incluso inferiores al de carteras con 100 empresas. En la práctica es posible encontrar alguno de estos subconjuntos, estudiando convenientemente las volatilidades y correlaciones de las empresas.
Por ejemplo, considerando las estrategias de baja volatilidad se consiguen carteras de tamaño moderado (10-20 empresas) con un VaR semanal de solo el 2.5%. Este VaR está por debajo de cualquiera de las carteras equiponderadas del gráfico anterior.
El siguiente gráfico evidencia aún más el efecto de la diversificación en el riesgo y la rentabilidad obtenida de nuestra cartera. Ahí se muestra el comportamiento en el espacio riesgo-rentabilidad de todas las carteras que he considerado en el experimento: 100 carteras distintas para cada uno de los 6 tamaños. Podéis ver la entrada “Comparación eficiente de estrategias de inversión” donde se introduce este gráfico.
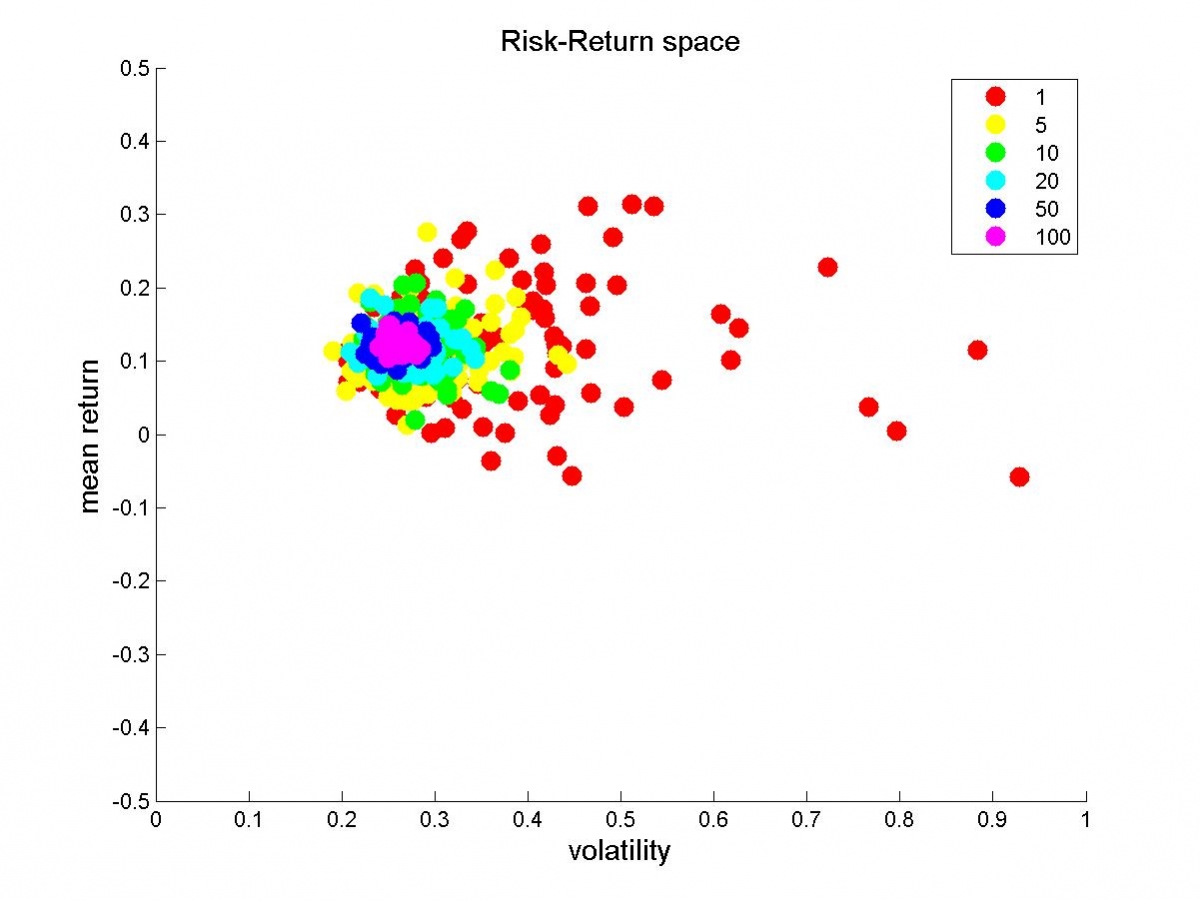
En el gráfico aparecen 600 puntos (carteras) agrupados por color (cada color representa un tamaño de cartera). Por ejemplo, un determinado punto rojo representa el riesgo (volatilidad) y la rentabilidad media, obtenidos en los últimos 5 años, de una cartera que escoge al azar una única empresa. Se puede observar el comportamiento errático de este tipo de carteras tan poco diversificadas. La volatilidad oscila entre el 20% y el 100%, y la rentabilidad oscila entre el -10% y el 30%.
Pero según aumentamos el número de empresas, se observa que el comportamiento tiende a concentrarse en una zona concreta. Por ejemplo, los puntos rosas representan el comportamiento de las carteras de tamaño 100. La volatilidad de estas carteras está concentrada alrededor del 25%, y la rentabilidad alrededor del 12.5%.
Este es el efecto de la diversificación: se reduce el riesgo sin renunciar a la rentabilidad.
El siguiente gráfico lo ilustra mejor. Cada punto ahora representa el centro del grupo al que pertenece. Esto es, el nuevo punto rojo representa el centro de la nube de puntos rojos del gráfico anterior.
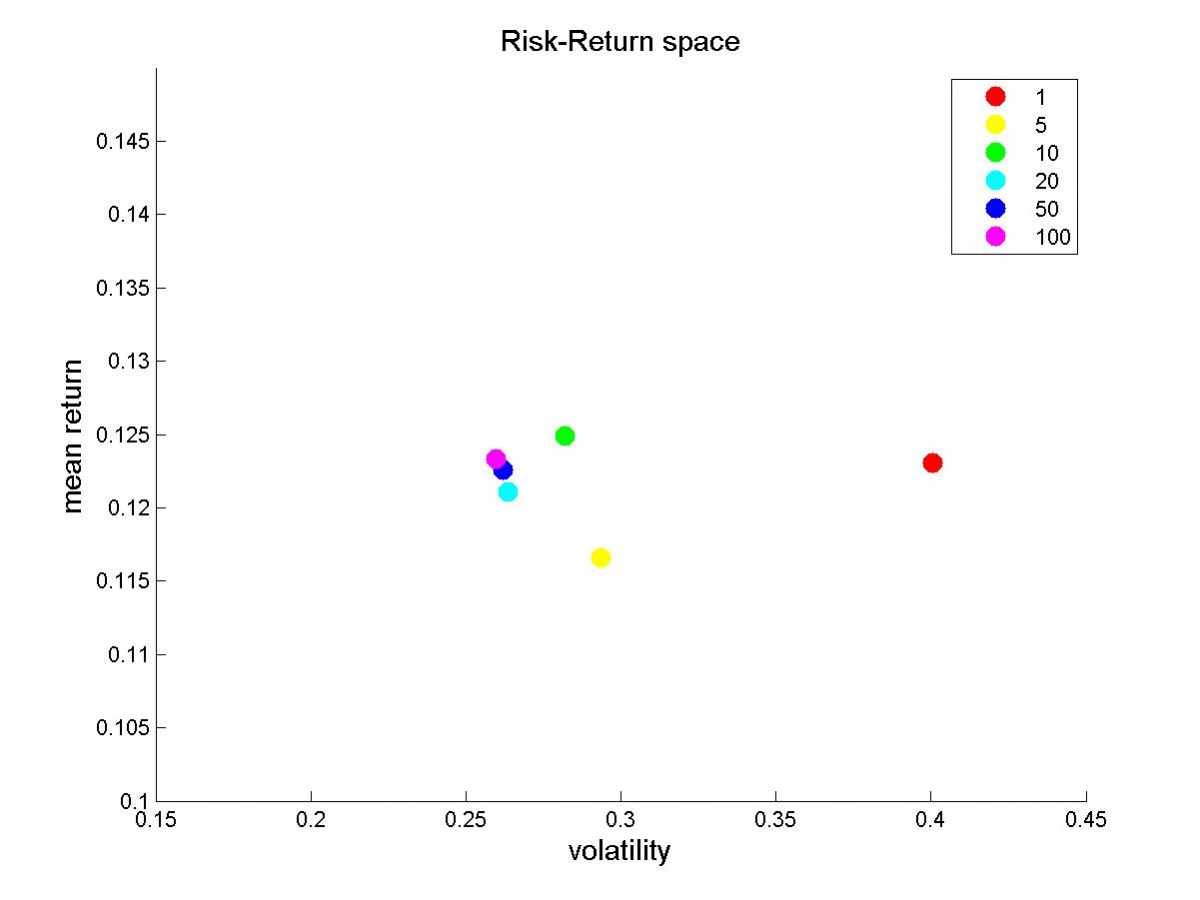
Se observa claramente cómo, a medida que aumentamos el tamaño de nuestra cartera, el riesgo disminuye, pero la rentabilidad no.
En resumen, tener un amplio abanico de empresas ayuda a reducir el riesgo sin renunciar a la rentabilidad esperada. Y no hace falta que el número de empresas sea muy alto, siempre que se escojan empresas con dependencias (correlaciones) no muy fuertes entre sí. Pero cuidado, que en épocas de crisis las correlaciones se disparan!
