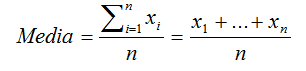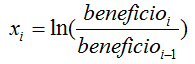En los dos artículos que podréis leer sobre la estimación del crecimiento futuro de una empresa, veremos diferentes métodos para lograr un pronóstico lo más certero posible. En este primer artículo veremos como utilizar la tasa de crecimiento histórico, con sus diferentes formas de cálculo. En la segunda parte del artículo, veremos cuando es recomendable usar las estimaciones de crecimiento de los analistas y, finalmente, tendremos en consideración los aspectos cualitativos del crecimiento de las empresas, que posiblemente es la parte más importante del proceso de estimación del crecimiento futuro de una empresa.
El Crecimiento Histórico
Cuando queremos estimar el crecimiento futuro de una empresa, generalmente el primer paso es observar la evolución histórica del crecimiento de la compañía. Aunque no siempre el crecimiento pasado es un buen indicador del crecimiento futuro de la empresa, puede contener información valiosa para estimar el futuro crecimiento. Hay diferentes medios para calcular el crecimiento medio histórico, cada uno con sus pros y sus contras. Los más usados son la media aritmética y la media geométrica.
La media aritmética se calcula como el promedio de las tasa de crecimiento pasadas de la empresa. Es decir, la media de toda la vida. El principal argumento a favor del uso de la media aritmética es su simplicidad. Su principal problema es que no tiene en cuenta el efecto de composición del crecimiento de los beneficios. La fórmula de la media geométrica es:
siendo “x” el crecimiento en el año “i” y “n” el número de años de la muestra.Ante el problema de que la media aritmética no tiene en cuenta la el crecimiento compuesto de la empresa, la solución es utilizar la media geométrica. Para calcular la media geométrica yo utilizo “la media de los logaritmos neperianos de crecimiento anual”. En otras palabras, la misma fórmula que en la media geométrica pero siendo:
AVISO: Una vez calculada la media de los logaritmos neperianos del crecimiento anual, hay que volver a transformar el resultando que tenemos en base logarítimica de la forma que podéis ver en el archivo de ejemplo que tenéis a continuación.
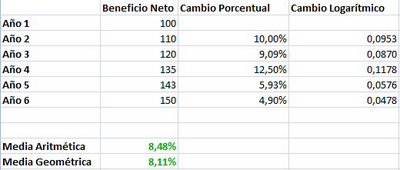
Un ejemplo claro de la diferencia que supone el uso de la media geométrica y la aritmética se puede observar en los siguientes ejemplos. En el primer ejemplo podemos ver una compañía en la que el crecimiento es más o menos constante a lo largo de los años.
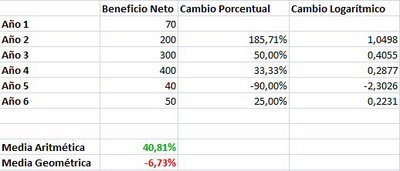
Como se puede apreciar, apenas hay diferencia entre la media aritmética y la geométrica. Sin embargo, veamos lo que sucede en una empresa con alta volatilidad en el beneficio neto.
En este ejemplo podemos ver que con el uso de la media aritmética el crecimiento histórico de la compañía es de más del 40%. Sin embargo, si usamos la media geométrica podemos ver que en realidad esta empresa ha reducido su beneficio neto a un ritmo de un 6,73% anual.
Aquí os dejo el archivo de Excel en el que podéis ver los cálculos realizados. Aunque el uso de medias geométricas pueda parecer difícil de comprender en teoría, en la práctica podemos ver que si usamos una hoja de cálculo se convierte en un proceso de lo más simple.
Otro método para calcular la tasa de crecimiento histórico para los que estéis familiarizados con la econometría es la regresión linear mediante el método de Mínimos Cuadráticos Ordinarios (también conocido como OLS por sus siglas en inglés). La forma de calcular la tasa de crecimiento histórico con este método es mediante una regresión linear del logaritmo neperiano del crecimiento de los beneficios. Para los que no lo estéis no pasa nada, ya que los métodos anteriores son igualmente válidos, aunque el usado en los textos académicos sea este al ser considerado más preciso técnicamente.
Para finalizar la primera parte de este artículo me gustaría comentar la utilidad del uso del crecimiento histórico para predecir el crecimiento futuro. El uso de las tasas históricas de crecimiento puede resultar útil en empresas con baja volatilidad en los beneficios siempre que esperamos que su evolución permanezca aproximadamente constante a lo largo de los próximos años. Por lo tanto, el uso del crecimiento histórico no es recomendable si prevemos que el entorno empresarial que envuelve a la compañía puede cambiar en los próximos años, aumentando o disminuyendo la tasa histórica de crecimiento.