Buenas noches.
Hoy, de nuevo, han aparecido comentarios interesantes respecto a lo que se está hablando aquí. Pero, si no os importa, y para no perder el hilo, hoy continuaré con el tema que había comenzado, y, en la próxima ocasión, hablaremos de las cuestiones que quedan pendientes, y de las que puedan salir mientras tanto.
Hoy, tenemos que hablar un poco de estadística. Cuando se trabaja con opciones, es imprescindible tener algunas nociones de estadística, ya que es ésta la que se utiliza para calcular el riesgo. Lo hacen las compañías de seguros a la hora de establecer las primas para sus pólizas, y lo hacen los compradores y vendedores profesionales de opciones.
La distribución normal.
Cuando hablábamos de la forma de calcular la volatilidad, comentamos que las cotizaciones de un valor, constituían una serie numérica. Una serie numérica, no es más que una lista de cifras. Ejemplos de series numéricas, hay innumerables: edades de los habitantes de una población, estaturas de los mismos, números premiados con el gordo de la lotería... o cotizaciones de valores de bolsa.
Cuando tenemos una serie numérica, es posible que algunos números se repitan. En ese caso, podemos agruparlos, y contar el número de veces que aparece cada número en la serie. Ese conteo, será una lista de dos variables: elemento de la serie y número de veces que aparece.
Ejemplo:
Serie numérica: 1, 3, 5, 3, 5, 5, 4, 1, 5, 5
Agrupación: (1,2), (3,2), (5,5), (4,1).
La agrupación, como se vé, tiene menos elementos que la serie, y ofrece la información de las veces que aparece en la serie numérica cada elemento. Esta agrupación, recibe el nombre de 'Distribución'.
Una distribución, tendrá una serie de propiedades y características, dependiendo de la naturaleza de los elementos de la serie a partir de la que se construye esa distribución.
De todas las distribuciones posibles, hay una de especial importancia estadística: se trata de la llamada distribución normal.
Para poder considerar que una serie numérica determinada es una distribución normal, es necesario aplicarle una batería de pruebas matemáticas. Cuando las cumplen, se concluye que tal serie es una distribución normal. Queda fuera del propósito de este blog, entrar en los pormenores de la decisión acerca de si una serie es una distribución normal o no.
Lo importante, son las propiedades que cumple una distribución normal. Son:
1. La serie numérica, tendrá una media. Por tanto, habrá elementos de la serie que serán mayores que la media, y elementos que serán menores.
2. La curva que forma su representación gráfica, tiene forma de Campana de Gauss.
3. Dicha curva, es asintótica al eje de abcisas (es decir, nunca llega a cero).
4. Además, es simétrica respecto de su media. Por tanto, la probabilidad de encontrar un dato en la serie mayor que la media, es igual a la de encontrar un dato menor que la media, es decir, el 50%.
4. Existe aproximadamente un 95% de probabilidades de que se observe un valor de la serie en el intervalo que va desde 2 veces la desviación estándar por encima de la media y 2 veces la desviación estándar por debajo de la media. En otras palabras: el 95% de los datos de la serie se encontrarán en el intervalo comprendido entre 2 desviaciones estándar y -2 desviaciones estándar (en realidad, el dato exacto para el 95% es 1,96 desviaciones estándar).
5. Como consecuencia del anterior, tan solo el 5% de los elementos de la serie se encontrarán a una distancia superior, por encima o por debajo de la media, de 2 veces la desviación estándar.
![Photobucket]()
Esta es la curva que presenta una distribución normal. La línea vertical del centro, es la media. La zona gris a la izquierda de la media es el área +2 veces la desviación estándar, y la de la derecha el área -2 veces la desviación estándar.
El 95% de los elementos de una serie que cumpla las condiciones de ser una distribución normal, estará comprendida dentro de ese área.
Hay que decir que la distribución normal perfecta solo existe como concepto matemático. Pero hay aproximaciones muy válidas, que cumplen las propiedades mencionadas.
Una de ellas, con las consiguientes consideraciones, lo constituye la serie numérica de las cotizaciones de un índice bursátil ponderado por capitalización.
Y a eso es a lo que vamos a intentar sacarle provecho.
Amenophis.
Hoy, de nuevo, han aparecido comentarios interesantes respecto a lo que se está hablando aquí. Pero, si no os importa, y para no perder el hilo, hoy continuaré con el tema que había comenzado, y, en la próxima ocasión, hablaremos de las cuestiones que quedan pendientes, y de las que puedan salir mientras tanto.
Hoy, tenemos que hablar un poco de estadística. Cuando se trabaja con opciones, es imprescindible tener algunas nociones de estadística, ya que es ésta la que se utiliza para calcular el riesgo. Lo hacen las compañías de seguros a la hora de establecer las primas para sus pólizas, y lo hacen los compradores y vendedores profesionales de opciones.
La distribución normal.
Cuando hablábamos de la forma de calcular la volatilidad, comentamos que las cotizaciones de un valor, constituían una serie numérica. Una serie numérica, no es más que una lista de cifras. Ejemplos de series numéricas, hay innumerables: edades de los habitantes de una población, estaturas de los mismos, números premiados con el gordo de la lotería... o cotizaciones de valores de bolsa.
Cuando tenemos una serie numérica, es posible que algunos números se repitan. En ese caso, podemos agruparlos, y contar el número de veces que aparece cada número en la serie. Ese conteo, será una lista de dos variables: elemento de la serie y número de veces que aparece.
Ejemplo:
Serie numérica: 1, 3, 5, 3, 5, 5, 4, 1, 5, 5
Agrupación: (1,2), (3,2), (5,5), (4,1).
La agrupación, como se vé, tiene menos elementos que la serie, y ofrece la información de las veces que aparece en la serie numérica cada elemento. Esta agrupación, recibe el nombre de 'Distribución'.
Una distribución, tendrá una serie de propiedades y características, dependiendo de la naturaleza de los elementos de la serie a partir de la que se construye esa distribución.
De todas las distribuciones posibles, hay una de especial importancia estadística: se trata de la llamada distribución normal.
Para poder considerar que una serie numérica determinada es una distribución normal, es necesario aplicarle una batería de pruebas matemáticas. Cuando las cumplen, se concluye que tal serie es una distribución normal. Queda fuera del propósito de este blog, entrar en los pormenores de la decisión acerca de si una serie es una distribución normal o no.
Lo importante, son las propiedades que cumple una distribución normal. Son:
1. La serie numérica, tendrá una media. Por tanto, habrá elementos de la serie que serán mayores que la media, y elementos que serán menores.
2. La curva que forma su representación gráfica, tiene forma de Campana de Gauss.
3. Dicha curva, es asintótica al eje de abcisas (es decir, nunca llega a cero).
4. Además, es simétrica respecto de su media. Por tanto, la probabilidad de encontrar un dato en la serie mayor que la media, es igual a la de encontrar un dato menor que la media, es decir, el 50%.
4. Existe aproximadamente un 95% de probabilidades de que se observe un valor de la serie en el intervalo que va desde 2 veces la desviación estándar por encima de la media y 2 veces la desviación estándar por debajo de la media. En otras palabras: el 95% de los datos de la serie se encontrarán en el intervalo comprendido entre 2 desviaciones estándar y -2 desviaciones estándar (en realidad, el dato exacto para el 95% es 1,96 desviaciones estándar).
5. Como consecuencia del anterior, tan solo el 5% de los elementos de la serie se encontrarán a una distancia superior, por encima o por debajo de la media, de 2 veces la desviación estándar.
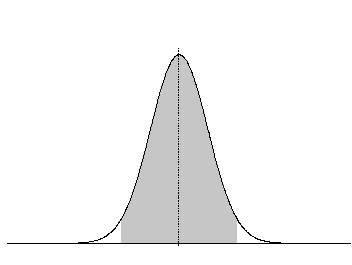
Esta es la curva que presenta una distribución normal. La línea vertical del centro, es la media. La zona gris a la izquierda de la media es el área +2 veces la desviación estándar, y la de la derecha el área -2 veces la desviación estándar.
El 95% de los elementos de una serie que cumpla las condiciones de ser una distribución normal, estará comprendida dentro de ese área.
Hay que decir que la distribución normal perfecta solo existe como concepto matemático. Pero hay aproximaciones muy válidas, que cumplen las propiedades mencionadas.
Una de ellas, con las consiguientes consideraciones, lo constituye la serie numérica de las cotizaciones de un índice bursátil ponderado por capitalización.
Y a eso es a lo que vamos a intentar sacarle provecho.
Amenophis.
3