En esta primera entrada os hablaré de la base de todo: la Teoría Moderna de Carteras, desarrollada por H. Markowitz en los años 50, y por la que ganó el Premio Nobel de Economía en 1990.
El concepto básico de esta teoría es la diversificación. Esto es, supongamos que tenemos 1200 euros y los queremos invertir bien en el B. Santander o bien en el BBVA. Pensamos que ambos bancos tendrán la misma rentabilidad esperada y los mismos niveles de riesgo. ¿Qué será mejor, invertir 1200 euros en SAN, o invertir 600 euros en SAN y los otros 600 en el BBVA?
Aquí la respuesta está clara: invirtiendo 600 euros en cada empresa conseguiremos la misma rentabilidad esperada pero con un riesgo menor. O sea, tenemos lo mismo que ganar pero menos que perder. Esta es la principal ventaja de tener una cartera de inversión.
La siguiente cuestión es: ¿se puede reducir aún más el riesgo en nuestra cartera de 1200 euros? Pues en principio sí, y de forma sencilla. Básicamente hay dos formas. La primera se refiere al tipo de empresas que compondrán nuestra cartera. Por ejemplo, nuestra primera cartera consiste en tener 600 euros en SAN y otros 600 en BBVA. Pero también pensamos que Telefónica puede tener la misma rentabilidad esperada y el mismo riesgo que esos dos bancos. Entonces, ¿nos quedamos con la cartera anterior, o con la siguiente cartera? 600 euros en SAN y los otros 600 en TEF.
Aquí la respuesta ya no es tan clara. Pero es mejor la segunda cartera que la primera. La razón es que el riesgo de la cartera no solo depende del riesgo de las tres empresas consideradas (que asumimos es el mismo), sino también de cómo las tres empresas interactúan entre sí. Como SAN y BBVA pertenecen al mismo sector, sus rentabilidades estarán muy ligadas y no reduciremos mucho el riesgo de nuestra cartera si tenemos a ambas presentes. Por el contrario, como SAN y TEF pertenecen a sectores distintos, sus rentabilidades no estarán tan ligadas y ello nos ayudará a reducir algo más el riesgo de nuestra cartera. Y siempre manteniendo el mismo nivel de rentabilidad esperada.
La segunda forma de reducir el riesgo de nuestra cartera es muy sencilla: simplemente añadir más empresas a la misma. O sea, es mejor invertir 400 euros en SAN, 400 en BBVA y los otros 400 en TEF. Y en principio cuantas más empresas mejor. Pero aquí ya hay que tener cuidado.
Estamos asumiendo que las empresas consideradas tienen la misma rentabilidad esperada y el mismo riesgo. Evidentemente esto en la práctica no es verdad. Cada empresa tendrá asociada una rentabilidad esperada (en función de su valor, sus ventas, su política empresarial, etc.) y un riesgo asociado (de mercado, de crédito, etc.). Además, las compañías entre sí presentarán distintas dependencias. Esto va a afectar a nuestra elección de las empresas que compondrán nuestra cartera, así como a la cantidad a invertir en cada una de ellas.
La formalización de estas ideas la desarrolló H. Markowitz en los años 50. Él propuso una teoría de inversión para encontrar una cartera que tenga una rentabilidad esperada máxima dado un determinado riesgo, o bien con un riesgo mínimo dada una determinada rentabilidad esperada. Tened en cuenta que no se puede encontrar una cartera con una alta rentabilidad y a la vez un bajo riesgo. Los dos objetivos están contrapuestos. Este es el famoso binomio riesgo-rentabilidad en finanzas: si quieres conseguir una mayor rentabilidad será a costa de asumir un mayor riesgo.
Por tanto, lo que propuso Markowitz fue una estrategia de inversión con un buen balance entre riesgo y rentabilidad. Y esta estrategia da lugar a una cartera bien diversificada.
A continuación os comentaré los aspectos básicos para encontrar esa cartera. Lo haremos con una inversión en 4 empresas: Santander, BBVA, Iberdrola y Telefónica.
El siguiente gráfico muestra la evolución de los precios de estas empresas a lo largo de 3 años determinados (156 semanas). Nosotros estamos en la semana 156 del gráfico y queremos invertir nuestro dinero de la semana 157 a la semana 180. Simplemente por ilustrar, basaremos nuestra decisión en la información proporcionada en el gráfico.
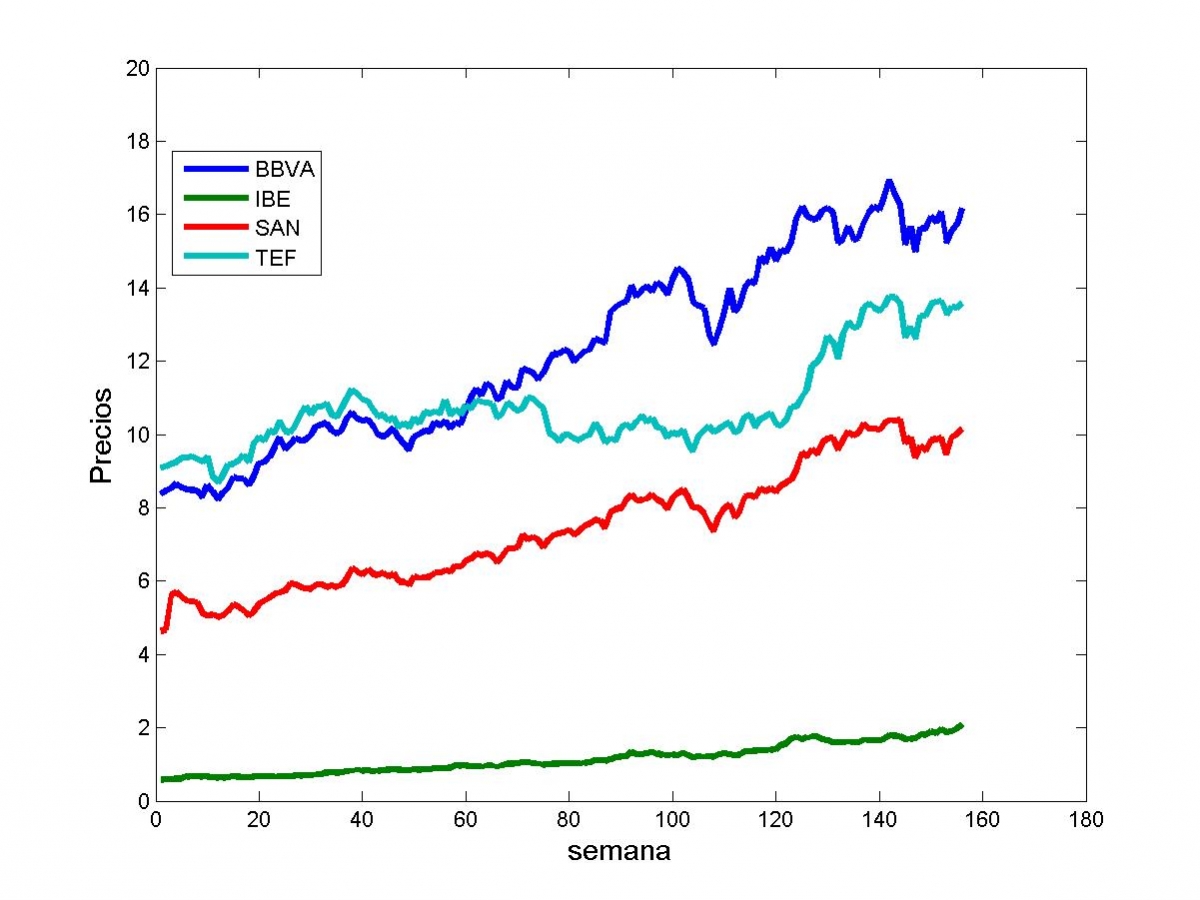
Si lo que nos interesa es conseguir la máxima rentabilidad esperada (de la semana 157 a la 180), entonces parece que deberíamos invertir todo nuestro dinero en BBVA. Pero por otra parte parece la opción con más riesgo o volatilidad.
Si lo que nos interesa es conseguir el menor riesgo posible en ese mismo periodo, entonces parece que lo más sensato es invertir todo nuestro dinero en IBE. Pero parece que es la opción menos rentable.
La teoría de carteras encuentra un compromiso entre los dos extremos anteriores. Por curiosidad, veamos cuál fue la evolución de los precios en las semanas 157-180. Por supuesto, esa evolución es la que nunca veremos en el momento de tomar la decisión de invertir.
.jpg)
A posteriori, hubiese sido mejor invertir todo en IBE: así hubiésemos conseguido la mayor rentabilidad, no esperada sino real. Pero como no somos adivinos, tenemos que tomar decisiones solo en base a la información que tengamos hasta ese momento, pero siempre teniendo en cuenta que se pueden dar situaciones como la del gráfico anterior.
Dicho de otra forma, es necesario encontrar un buen balance entre la rentabilidad esperada en nuestro periodo de inversión y el riesgo que queremos asumir.
¿Pero cómo medir la rentabilidad esperada? ¿Y el riesgo?
En la siguiente entrada veremos, con la ayuda de unas pequeñas matemáticas, cómo formalizar estos conceptos.

