En esta entrada continuaremos con los conceptos básicos de diversificación, aunque nos hace falta la ayuda de unas pequeñas matemáticas, pero se entienden muy bien.
En primer lugar, necesitamos calcular la rentabilidad en bolsa de una empresa en un determinado momento, t. Es simplemente el cambio porcentual del precio respecto al periodo anterior, t-1. En términos matemáticos, la rentabilidad en el periodo t es:
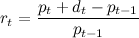
Donde p denota el precio de la empresa, y d es el posible dividendo pagado en el periodo.
Estas rentabilidades se pueden calcular para todas las compañías hasta el momento, t, en el que se vaya a tomar la decisión de invertir. Pero a nosotros nos interesan las rentabilidades futuras, esto es, en periodos superiores a t. Como el futuro no lo conocemos, nos tenemos que conformar con estimar qué rentabilidades esperamos que tengan esas empresas en el futuro.
En subsiguientes entradas os comentaré más sobre este tema, pero básicamente se puede usar el análisis cuantitativo, técnico, fundamental, etc. para estimar dichas rentabilidades. Aunque he de decir aquí que las estimaciones de este tipo de análisis no suelen ser muy acertadas a lo largo del tiempo.
En el ejemplo de 4 empresas de la entrada anterior, supongamos que las rentabilidades (anuales) esperadas de estas empresas son:
|
|
BBVA |
IBE |
SAN |
TEF |
|
Rentabilidad esperada |
10% |
20% |
15% |
13% |
Nuestro interés está sobre todo en la rentabilidad esperada de la cartera. Si invertimos lo mismo en cada una de las cuatro empresas, la rentabilidad esperada de la cartera será
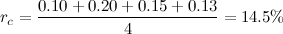
En general, dados unos pesos a cada empresa w, y dadas unas rentabilidades m, la rentabilidad esperada de una cartera se calcula como:
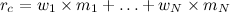
siendo N el número de empresas en nuestra cartera. Se puede observar que cambiando los pesos de la cartera, podemos aumentar o disminuir la rentabilidad esperada de la misma (de un 10% a un 20% en nuestro ejemplo). Pero esto no es gratis: será a costa de aumentar o disminuir el riesgo de la cartera. Pero, ¿cómo se calcula este riesgo?
Markowitz observó que el riesgo de la cartera no solo depende del riesgo de cada una de las empresas asociadas, sino también de la dependencia entre ellas. El riesgo se mide a través de la volatilidad. En posteriores entradas os hablaré sobre el cálculo de las volatilidades, pero básicamente mide cuál es la oscilación de la rentabilidad de una acción respecto a su valor esperado.
En el ejemplo que nos ocupa, supongamos que las volatilidades (anuales) de las cuatro empresas son:
|
|
BBVA |
IBE |
SAN |
TEF |
|
Volatilidad |
22% |
32% |
26% |
22% |
Por ejemplo, el BBVA tiene una rentabilidad esperada del 10% junto con una volatilidad del 22%. ¿Cómo se interpreta esta volatilidad? Significa aproximadamente que, con una probabilidad del 95%, podemos llegar a ganar hasta un 46% (con muy buena suerte), pero también podemos llegar a perder hasta un 26% (con muy mala suerte).
En cuanto a la dependencia entre empresas, se mide con la correlación. Es un valor porcentual, entre -1 y 1, que es mayor cuanto mayor es la relación entre dos empresas. En entradas posteriores hablaré sobre cómo estimar estas medidas de dependencia.
En nuestro caso, estas son las correlaciones entre cada par de empresas:
|
|
BBVA |
IBE |
SAN |
TEF |
|
BBVA |
1 |
0.18 |
0.91 |
0.62 |
|
IBE |
0.18 |
1 |
0.14 |
0.33 |
|
SAN |
0.91 |
0.14 |
1 |
0.58 |
|
TEF |
0.62 |
0.33 |
0.58 |
1 |
Como es de esperar, se observa que las dos compañías más relacionadas son BBVA y SAN. Esta alta dependencia no nos ayudará mucho en la reducción del riesgo de nuestra cartera. Las compañías que menos relación tienen son BBVA y IBE (esto era menos evidente). Esta baja relación sí nos puede ayudar a reducir el riesgo.
Ahora ya podemos deducir el riesgo de la cartera. Simplemente tenemos que sumar las varianzas (volatilidades al cuadrado) de cada empresa ponderadas por su peso al cuadrado, así como todas las dependencias cruzadas entre pares de empresa.
O sea, para el caso sencillo de una cartera con solo dos empresas (BBVA y IBE), la varianza de la cartera será (con los datos anteriores):
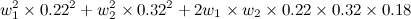
donde los w muestran los pesos de la cartera en las dos empresas. El cálculo para una cartera más grande se realiza de forma similar, introduciendo todas las dependencias por parejas como en el caso anterior.
Al igual que en el caso de la rentabilidad esperada de la cartera, cambiando los pesos de la misma, podemos aumentar o disminuir el riesgo de la cartera (de un 32% a un 22% en nuestro ejemplo). Pero de nuevo: será a costa de aumentar o disminuir la rentabilidad esperada de la cartera.
Por tanto ya tenemos las ideas básicas para calcular los pesos óptimos de nuestra cartera: fijamos un nivel de riesgo de cartera, p.e. del 15%, y buscamos aquella combinación que maximiza la rentabilidad esperada de la misma. O bien, fijamos una rentabilidad esperada para la cartera, p.e. del 20%, y buscamos aquella combinación que minimiza el riesgo de la misma. Ambos enfoques son equivalentes.
En función de nuestra aversión al riesgo (riesgo máximo asumido, o bien rentabilidad mínima esperada), tendremos distintas composiciones de nuestra cartera.
Por ejemplo, un inversor muy arriesgado, elegiría esta cartera:
w = (0, 1, 0, 0)
Esto es, invertiría todo en IBE. Por el contrario, un inversor muy poco arriesgado elegiría esta cartera:
w = (0, 0, 0.05, 0.95)
Esto es, casi todo en TEF, un poco en SAN, y nada en el resto.
Para aversiones al riesgo intermedias hay una infinidad de combinaciones óptimas posibles. Pero siempre subyace la misma idea: si queremos una cartera con una alta rentabilidad esperada será a costa de asumir un mayor riesgo.
Bueno, hasta aquí la teoría. Ahora viene lo más importante: ¿cómo se pone esto en marcha? y ¿funciona realmente?
Sobre la primera pregunta, es complicado. Con nuestras 4 empresas, tendríamos que estimar sus 4 rentabilidades esperadas, sus 4 volatilidades, y las 6 correlaciones entre ellas. Cada uno de estos 14 parámetros es muy difícil de estimar, especialmente las rentabilidades esperadas.
Pero si quisiéramos construirnos una cartera con los 35 valores del Ibex, entonces tendríamos que estimar ¡665 parámetros! Demasiado complicado para un inversor que no quiere complicarse mucho la vida.
¿Pero qué pasa si nos animamos a intentarlo? A continuación os muestro lo que pasaría si hacemos el siguiente back-testing: cada semana t del pasado calculamos la cartera de Markowitz (para un riesgo moderado), y a la semana siguiente t+1 calculamos la rentabilidad real obtenida. Repetimos este experimento un determinado número de semanas en el pasado (p.e. un año entero).
A continuación os muestro qué hubiese pasado si en un determinado periodo anual hubiésemos invertido un euro en la cartera de Markowitz y un euro en el Ibex35.
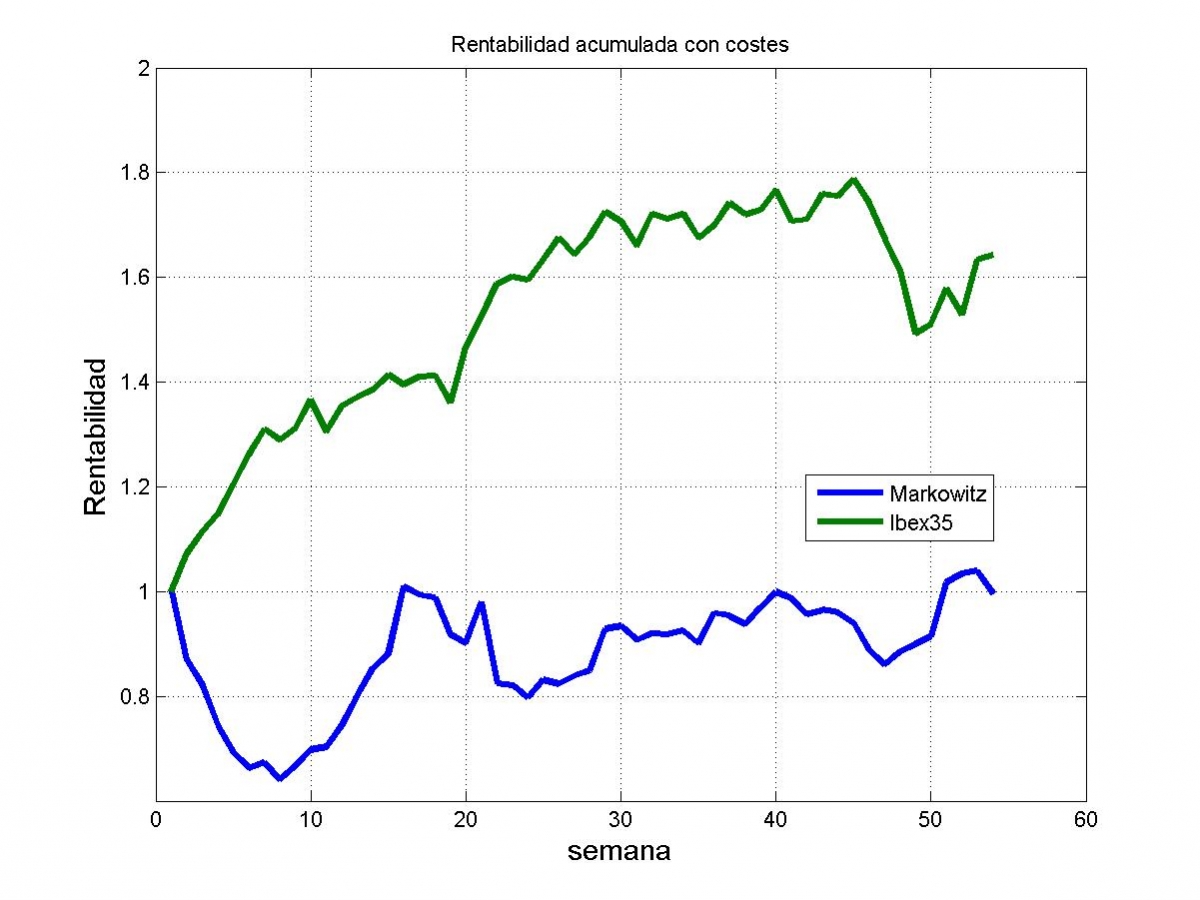
Con el Ibex hubiésemos ganado más de un 60% en ese determinado periodo. Con la cartera de Markowitz nos hubiésemos quedado igual al finalizar el periodo: o sea, un desastre.
¿Qué ha pasado? ¿Es errónea la teoría de Markowitz? ¿Es mejor invertir en un índice, como el Ibex35, y olvidarnos de todo?
Más adelante os responderé a estas preguntas, aunque os adelanto que algo interesante se puede hacer…
