Vamos con la Lección nº 8 del curso "Bienvenido al Mundo de las Opciones".
De momento hemos visto:
Lección 1: Introducción a las Opciones
Lección 2: Introducción a los Spreads de Opciones
Lección 3: Cadena de Opciones y Gráfico de Riesgo
Lección 4: Strikes y Valor de las Opciones
Lección 7: Ejecución-Asignación y Paridad Put/Call
En esta lección vamos ver algunos conceptos sobre las Letras Griegas. Y el viernes, en tu email, recibirás un video práctico sobre la lección de hoy. Para recibir este video privado, debes registrarte a SharkOpciones a través del siguiente link:
Quiero Registrarme al Curso Gratuito de SharkOpciones
Comenzamos...
8. Las Letras Griegas
En esta lección vamos a hablar de uno de los pilares básicos para gestionar opciones: las Letras Griegas.
Las Letras Griegas nos representan de forma numérica cuál es el riesgo de exposición de nuestra opción o spread a determinados parámetros de mercado. Cada letra griega nos dará información sobre un parámetro en concreto (volatilidad, desplazamiento, etc.).
Los principales parámetros que afectan al precio de una opción son los siguientes:
- Desplazamiento del subyacente; la letra griega asociada al mismo será Delta.
- Aceleración del propio desplazamiento del precio, representado por Gamma.
- Volatilidad implícita, que vendrá representada por Vega.
- Tiempo de expiración, representado por Theta.
- Cambios en los tipos de interés, representado por Rho.
- Dividendos del subyacente, sin letra griega.
Podemos encontrar también otro rango de letras griegas mucho menos conocidas, como Charm, DvegaDtime, Color, Vanna, Vomma y Zomma, en la que no vamos a entrar en detalle ya que no sirven de nada al "retail trader".
De igual forma, no entraremos a valorar Rho, ya que los cambios en los tipos de interés es un fenómeno que no se da con frecuencia, por lo que su impacto en el precio no es relevante.
En resumen, en estas próximas dos lecciones nos centraremos en las 4 letras griegas más importantes y que son las que todo operador de opciones debe tener en cuenta: Delta, Gamma, Vega y Theta. Para esta lección empezaremos con Delta y Gamma.
8.1 Delta
Delta es la letra griega que nos dice cuánto se va mover el precio de nuestra opción o estrategia en función del movimiento del subyacente.
El valor de delta oscila de 0.0 a 1.0 para las opciones Calls, y de 0.0 a -1.0 para las opciones Puts. En ambos casos, opciones compradas, ya que vendidas toman el signo contrario.
Por ejemplo, si mi opción tiene un delta de 0.6, significa que mi opción subirá $0.60 por cada $1.0 que suba el subyacente.
En la cadena de opciones, los valores de las letras griegas los encontramos en formato unitario, pero si introducimos un contrato, el delta de 0.6 sería de 60, si introducimos 10 contratos tendríamos 600 deltas, y así sucesivamente. A mayor delta, mayor beneficio obtendremos si el movimiento acompaña, y mayor será la pérdida si el subyacente va en contra a nuestro delta.
Si tuviéramos que hacer un ranking de importancia, delta sería la griega más importante pues está afectada directamente por el movimiento del precio de la acción.
Probabilidades
Delta también se usa como indicador de probabilidades. No es del todo correcto, pero es muy aproximado.
Por ejemplo, si el delta de mi opción es 0.30, significaría que las probabilidades de que mi opción expire ITM (in the money) son del 30%
Calls y Puts
Hemos visto que el delta para las Calls (compradas) es positivo. Eso significa que mi opción Call va a generar valor siempre y cuando el subyacente suba. De igual forma, si tengo una estrategia spread con un delta neto positivo, también generará valor cuando el subyacente suba.
Y el delta de las Puts (compradas) es negativo, lo que significa que me interesa que el precio del subyacente baje, ya que mi opción o estrategia generará valor cuando dicho subyacente baje, debido a ese delta negativo.
Variaciones de Delta
El delta varía en función de su posición en la cadena de opciones. Como referencia, delta suele ser 0.5 en la posición ATM y aumenta según entramos ITM y disminuye según salimos OTM. Y su variación de cambio en dicha cadena depende del valor de Gamma, que lo veremos en el siguiente post.
Delta también depende de la volatilidad y del tiempo.
Delta, en la fecha de expiración, es 0 ó 1, es decir, la opción expira ITM o OTM.
Matemáticas
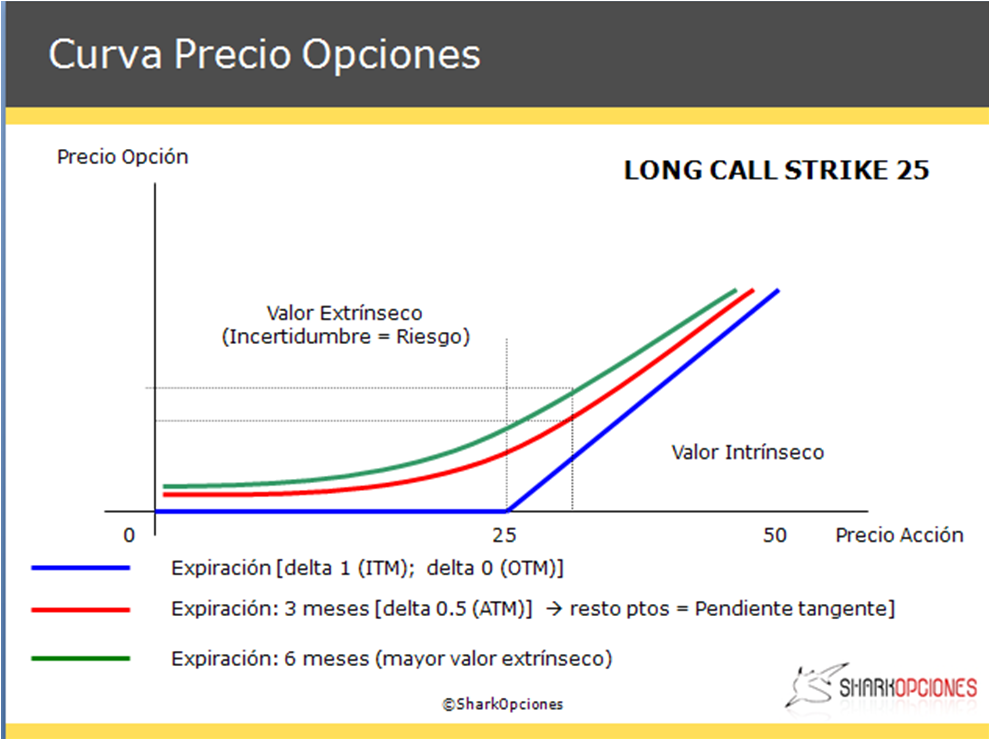
Y por último, como relación matemática, Delta es la pendiente de la tangente que genera el gráfico del precio de la opción.
En la fecha de expiración, las opciones ITM (con valor intrínseco) tendrán una pendiente de 45º, lo que significa que su delta es 1, mientras que las opciones OTM (sin valor) tendrán una pendiente de cero, lo que significa que su delta es 0 (para el gráfico de una Long Call).
En el gráfico siguiente podemos observar cómo la curva se hace más plana en función de la fecha de expiración, lo que significa que la pendiente de la línea tangente que se forma va variando y, por ende, el delta obtenido también será distinto.
8.2 Gamma
Gamma es una de las letras griegas con mayor importancia pero que, bajo mi punto de vista, está un poco olvidada o no es muy considerada.
Gamma nos mide el ratio de cambio de delta. Se expresa en tanto por ciento y nos indica lo que se mueve delta en función del movimiento del subyacente. Es decir, nos mide la aceleración de delta. Es el delta del propio delta.
Gamma es máxima en la zona ATM y disminuye para los strikes ITM y OTM.
Por ejemplo, si tenemos una opción con un delta de 0.50 y un gamma de 0.04 (4%), y el subyacente se mueve +$1, significa que delta variará de 0.50 a 0.54. Si por el contratio la acción baja -$1, entonces delta variará a 0.46
Gamma es un número positivo para las opciones LONG (LC o LP) y un número negativo para las opciones SHORT (SC o SP).
Si estamos largos en Gamma, nos interesa que el precio del subyacente se mueva, mientras que si estamos cortos en Gamma, nos interesa un mercado lateral.
Variación de Gamma
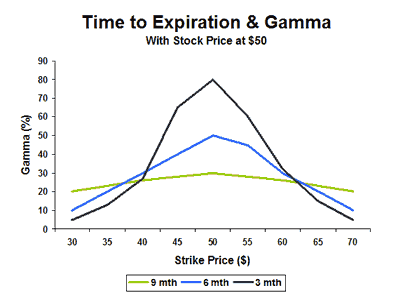
Gamma varía en función del tiempo de expiración, en función de la volatilidad y en función del movimiento del precio. Sobre éste último, ya hemos comentado arriba que a medida que el precio strike entra ITM o OTM, el valor de gamma disminuye.
En cuanto a la fecha de expiración, el valor de gamma se incrementa muchísimo en strikes ATM en las fechas más próximas, mientras que en expiraciones más alejadas, dicho valor de gamma se reduce (en la siguiente imagen se podrá entender mejor).
Debido a esta característica, el conocido "Gamma Risk" se produce cuando tenemos opciones Short ATM y con una fecha de expiración próxima. Debido al elevado gamma, la variación de delta será muy grande, de forma que cualquier ligero movimiento del precio hará que nuestra SC o SP entre ITM. Lo que significa que de una posición ganadora entraríamos en una posición perdedora simplemente por un ligero movimiento del precio.
Por ello, mi recomendación es que si tienes opciones Short ATM en la última semana de expiración, debes rollarlas (exceptuando que tu estrategia contemple la asignación).
Y otro tipo de variación a tener en cuenta es con la volatilidad. Si observas la variación de gamma en dos acciones con diferente volatilidad, podrás comprobar que para la menos volátil, la diferencia entre el gamma ATM y el gamma ITM-OTM es muy pronunciada, mientras que para la más volátil, el valor de gamma es prácticamente constante en todos los strikes.
El motivo es que el valor extrínseco de las opciones OTM o ITM en acciones volátiles ya de por sí es elevado, de forma que según se aproximan hacia la zona ATM, el incremento de ese valor extrínseco es mínimo, mientras que para las acciones poco volátiles, ese incremento es más acusado.
En el video del viernes, veremos aplicaciones prácticas de estos conceptos.
Feliz semana!!
Curso Gratuito - "Bienvenido al Mundo de las Opciones"
SharkOpciones
********************************
Formación en Inversión y Trading con Opciones: Registro gratuito aquí
