Buenas noches a tod@s,
Este post aborda aquellos parámetros y variables que afectan a la que suele ser la griega más importante de todas en una cadena de opciones: Delta.
Repasando el concepto de delta tenemos que es la griega que mide la variación del valor de la opción ocasionada por una variación en el precio del activo subyacente. Por ello matemáticamente es la primera derivada del valor de la opción con respecto al precio de dicho activo subyacente. Siendo V en la imagen adjunta el valor de la prima de la opción y S el precio del activo subyacente,
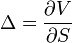
En opciones vanilla nos indica también aproximadamente la probabilidad de que la opción termine en dinero. Y también nos ayuda a utilizar la opciones como instrumento de cobertura si tenemos una posición en el subyacente. Pero la delta de una opción no suele ser constante durante mucho tiempo. Puede cambiar afectada por tres motivos:
1. Cambios en el precio del activo subyacente:
A medida que cambia el precio del activo subyacente, la delta de la opción suele cambiar. Si consideramos una call a dinero con una delta de 0,5 tendrá una probabilidad aproximada de un 50% de expirar dentro de dinero. Si el precio del activo subyacente se incrementa, la probabilidad de expirar en dinero de dicha call a su vez aumentará por lo que su delta será superior también a 0,5. Para saber en que medida la delta de una opción va a cambiar, tenemos que mirar a gamma. Gamma mostrará el cambio producido en la delta de la opción ante un cierto cambio en el precio del activo subyacente.
Gamma es matemáticamente la segunda derivada del valor de la opción respecto al precio del activo subyacente. Todas las opciones compradas tienen gamma positiva y todas las opciones vendidas tienen gamma negativa. Gamma es mayor en opciones a dinero y disminuye según nos alejamos del dinero, bien sean opciones en dinero o fuera de dinero. Gamma disminuye también según pasa el tiempo, en el supuesto de que el precio del activo subyacente y la volatilidad implícita de la opción permanezca estable. Gamma asimismo variará si varía el nivel de volatilidad implícita.
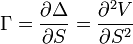
Si intentamos también un sistema de coberturas del tipo delta neutral, es importante neutralizar la gamma de la posición. Ello garantizará que delta se mantendrá neutral para una amplia variación en el precio del activo subyacente.
2. Cambios en el nivel de volatilidad implícita de la opción:
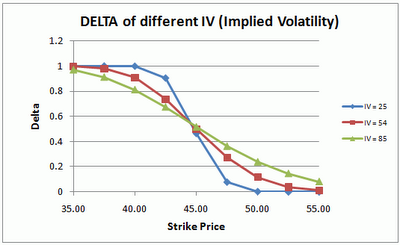
Supongamos que la volatilidad implícita de una call con una delta de 0,1 es del 25%. Imaginemos ahora que aumenta la volatilidad implícita de esa misma call a un 50%. Ello se puede interpretar como que el precio del activo subyacente será aproximadamente dos veces más volátil. Por ello es de esperar que la delta de la call aumente, ya que a mayor volatilidad del activo subyacente, mayor será la probabilidad de que la call expire en dinero (recordemos que delta mide aproximadamente la probabilidad de expiración en dinero de dicha call).
Gamma es la griega de segundo orden que nos dice cómo cambia delta cuando cambia el precio del activo subyacente. Vanna es a su vez la griega de segundo orden que mide cuanto cambia delta ante una variación en la volatilidad implícita de la opción. Vanna también se denomina DdeltaDvol. Matemáticamente es la derivada de segundo orden del valor de la opción, una vez respecto al precio del activo subyacente y otra vez respecto a la volatilidad implícita de la opción. DdeltaDvol viene a significar la sensibilidad del delta de la opción con respecto a cambios en la volatilidad implícita. Vanna puede ser útil para controlar la sensibilidad de un portfolio de opciones delta neutral ayudando a anticipar los cambios en la delta global ante cambios en la volatilidad.
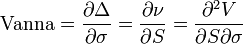
Por lo general, vanna asume una forma normalizada para mostrar el cambio en el delta ante un movimiento de un 1% en la volatilidad implícita. Las call tienen vanna positivo y las puts tienen vanna negativo. Esto se debe a que un aumento de la volatilidad implícita plantea la posibilidad de que cualquier compra o venta expire en el dinero, y esto es sinónimo de una mayor y absoluta delta.
3. Paso del tiempo:
La delta de una opción suele cambiar ante el paso del tiempo.
Una opción con una delta del 10% tendrá un delta diferente dentro de un mes, aunque permanezca el mismo nivel de precios el activo subyacente y su volatilidad implícita fuera la misma. En la práctica la volatilidad implícita de una opción sobre todo si no se halla a dinero, también suele cambiar según pasa el tiempo. El tiempo erosiona el valor extrínseco de las opciones y ello lógicamente también afecta a la delta de la opción y es fácil entender porque. Una opción con un delta de 10% se puede considerar que tiene aproximadamente una probabilidad del 10% de expirar en dinero. Pero si el precio del subyacente no se mueve y el nivel de volatilidad implícita se mantiene, la probabilidad de que esta opción expire en dinero disminuirá. Además recordemos que a vencimiento, todas las deltas de las opciones fuera de dinero son cero. Así que entre el momento actual y la expiración, delta va a cambiar simplemente porque el tiempo pasa.
Este efecto puede ser más importante en los días cercanos al vecimiento. Si tenemos un portfolio de opciones delta neutral que se está acercando a vencimiento, entonces incluso el paso del fin de semana puede tener importancia.
La griega de segundo orden que mide los cambios del delta con respecto al paso del tiempo se denomina charm. Charm también se denomina DdeltaDtime. Matemáticamente charm es la derivada de segundo orden del valor de opción, una vez respecto al precio del activo subyacente y otra vez respecto al paso del tiempo. También es entonces la derivada de theta con respecto al precio del activo subyacente. Además siempre tiene valor negativo.
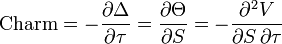
El resultado matemático de la fórmula para charm se expresa en delta / año. A menudo es útil dividir por el número de días el año para llegar a la decadencia de delta por día. Este uso es bastante exacto cuando el número de días que quedan hasta la expiración de la opción es grande. Cuando una opción se acerca a vencimiento charm cambia cada vez más rápidamente.

Hay otros factores que pueden afectar a delta pero estos serían los tres principales, e incluso el más importante de los tres el primero que mencioné, los cambios en el nivel de precios del activo subyacente.
A continuación el video siguiente analiza la importancia de gamma al mantener un portfolio de opciones delta neutral
Y un repaso a las principales griegas en el marco del modelo Black Scholes
Saludos
