Hasta ahora hemos visto que conviene tener un sistema de trading para generar señales de entrada y salida y tener así una operativa regular con las ventajas que tiene el uso de sistemas automáticos. Hemos visto cómo podemos saber si tenemos un sistema rentable y también que interesa combinar sistemas para poder reducir el drawdown mientras que se acumulan los beneficios de los sistemas individuales.
Pero nada de esto tiene sentido sin un control estricto del riesgo. Esto es lo que hace la gestión de capital o Money Management. Se ocupa de decir cuánto hay que arriesgar en la próxima operación. Es una pieza tan importante de una buena operativa que incluso uno puede arruinarse con un buen sistema (estadísticamente fiable) si se excede con el riesgo. Podríamos definir Gestión de Capital como el cálculo de cuánto es lo idóneo a arriesgar en la próxima operación.
Evidentemente al operar un sistema es primordial calcular y aplicar la cantidad óptima que debemos arriesgar en cada operación para maximizar el beneficio neto total. Si pudiéramos saber a priori el resultado de la siguiente operación entonces la cantidad óptima sería cero si la siguiente operación es una pérdida y sería el 100% de nuestro capital si la operación siguiente es una ganancia. Desafortunadamente nuestro intermediario no nos permite operar en el centro del gráfico sino a la derecha del todo, donde la siguiente barra está por venir y no hay forma de saber si será alcista o bajista.
Supongamos que disponemos de un sistema que nos permite acertar la mitad de las veces. Cuando acertamos, en promedio somos capaces de ganar un 20% y cuando fallamos, en promedio somos capaces de cortar las pérdidas al 3%. ¿Cuál es nuestra rentabilidad promedio?
Rentabilidad = 0.5*20-0.5*3 = 8.5%
Bajo las condiciones de este problema tendremos una rentabilidad positiva del 8.5%. El cálculo es simplemente multiplicar cada ocurrencia por su probabilidad. El resultado final es la ganancia media en tanto por ciento, o expectativa del sistema.
Expectativa
La expectativa matemática es la cantidad que se espera ganar o perder en promedio en cada operación. Un operador no debería operar en el mercado a no ser que sepa con certeza que el sistema que va a utilizar tiene expectativas positivas.
Lo bueno de la expectativa es que junta en un solo estadístico el porcentaje de aciertos con la tasa ganancia/pérdida proporcionando así un dato que nos dice si nuestro sistema genera dinero o no, en promedio. Así de simple y efectivo. La expectativa se calcula multiplicando la cantidad ganada o perdida por su probabilidad asociada.
Supongamos un sistema que tiene las siguientes estadísticas:
- Porcentaje de aciertos: 90%
- Ganancia promedio: 275 euros
- Perdida promedio: 2700 euros
Muchos especuladores querrían tener un sistema como este, con un 90% de aciertos. Veamos cuales son las expectativas o resultado medio de este sistema:
0.90*275-0.10*2700=-22.5
Las expectativas son negativas. Este es un sistema con el que se acierta el 90% del tiempo y aun así se pierde dinero operando con él. En promedio se perderán 22.5 euros por operación.
Para calcular la expectativa de un sistema a partir de su porcentaje de aciertos y del ratio ganancia/pérdida se utiliza la siguiente expresión:
Expectativa = (1+B)*P-1
Donde B es el ratio ganancia/pérdida promedio (o Payoff Ratio) y P es el porcentaje de aciertos.
Veamos un ejemplo sencillo:
Un sistema de trading tiene un porcentaje de aciertos del 40% y un ratio ganancia/pérdida de 1.4. ¿Es rentable?
Expectativa = (1+1.4)*0.4-1=-0.04
Pues no, tiene una expectativa de 4 céntimos de euros en pérdidas por cada euro arriesgado. No hay ningún método de gestión de capital que consiga que este sistema gane dinero. Si no se pueden cumplir estos dos requisitos es mejor no operar.
La expectativa nos dice lo que se espera ganar por cada euro arriesgado. Un buen sistema tiene más de 50 céntimos de expectativa. Es decir que esperamos ganar medio euro por cada euro que arriesgamos. Un sistema con un porcentaje de aciertos del 40% y un ratio ganancia/pérdida de 3 es el típico caso de un sistema seguidor de tendencias, que acierta poco pero consigue una buena ganancia. Este sistema tiene una expectativa de 60 céntimos por cada euro arriesgado.
Hay una variable más involucrada en la evaluación de una metodología de trading que es tan importante como la expectativa. Es la oportunidad. ¿Con cuanta frecuencia podemos conseguir las operaciones?
Si un sistema tiene una expectativa de 60 céntimos por cada euro arriesgado pero solo genera 2 operaciones al año entonces no es una buena opción. Seguramente nos interese más un sistema ligeramente inferior (expectativa menor) pero que genere muchas más operaciones. Al final de un año la ganancia en euros del segundo sistema será mayor. Aquel cuyo producto de expectativa por oportunidad (número de operaciones) sea mayor será el que más dinero genere.
El lector puede notar que la expectativa es una “condición necesaria pero no suficiente”. Lo primero que debemos comprobar es que tenemos una expectativa positiva pero eso no nos garantiza ganar dinero. No nos garantiza la rentabilidad.
La gestión de capital comienza con un sistema con expectativa positiva, pero como se acaba de explicar eso es solo uno de los muchos requisitos necesarios para la rentabilidad. El propósito de este artículo no es entrar al detalle sobre la gestión de capital, que es un tema complejo con abundante contenido matemático. Para una información más detallada se remite al libro Cagigas “Trading con Gestión de Capital” que contiene mucha información que no es posible incluir aquí.
Ejemplo de evaluación de sistemas con datos reales. El Sistema Gustafson.
A continuación se va a diseñar y optimizar un sistema de trading con el objeto de mostrar las técnicas que hemos visto hasta ahora y poder comprobar así su validez estadística.
El sistema que vamos a implementar está basado en el sistema Gustafson que viene explicado en el libro Kaufman “New Trading Systems and Methods”. Gutafson afirma que el SP500 es un índice tan eficiente que normalmente no hace tendencias largas, así que tras varios días de subidas o de caídas el giro es muy probable. Así, se definen las siguientes reglas para crear un sistema de trading:
- Si el SP500 cae durante 4 días seguidos compramos
- Si el SP500 sube durante 4 días seguidos vendemos
- Una vez comprados nos salimos a los 8 días en cualquier caso
Estas son unas reglas bien simples que se basan en la poca direccionalidad que tiene el índice SP500 a la hora de hacer tendencias. Solo se opera en el lado largo (no hay posiciones cortas) y así se aprovecha el sesgo alcista que tienen los índices a largo plazo.
Cuando implementamos estas 3 sencillas reglas en un software de simulación (Amibroker) el resultado es el siguiente. La simulación se hace desde el año 2000 hasta el 2008, con un futuro grande del SP500 (250 dólares por punto).

Donde Net es la ganancia neta de 89.000 dólares. MSD es el máximo drawdown en porcentaje, que es del 29%, un valor aceptable. RF es el Recovery Factor. PF es el Profit Factor, que toma un valor bastante bueno de 1.81.
Aquí podemos ver lo que comentábamos con anterioridad respecto al ratio de Sharpe. Este sistema tiene un Sharpe = 1.3 así que estamos ante un buen sistema, independientemente de lo que digan los otros ratios. No obstante los demás ratios son bastante buenos. Por ejemplo, una ganancia promedio de 2.358 dólares por operación es algo muy beneficioso que compensa de sobra las comisiones y el deslizamiento (slippage) al introducir las órdenes en el mercado.
El porcentaje de aciertos del 63% es una característica muy deseable porque todos los sistemas que aciertan más de lo que fallan son psicológicamente más fáciles de operar y además nos permiten detener el sistema o ausentarnos de los mercados con la certeza de que cuando volvamos cada nueva operación seguirá teniendo una probabilidad mayor de salir bien que de salir mal. Los sistemas que aciertan poco pueden generar la operación ganadora que compensa las anteriores durante nuestras vacaciones, y por consiguiente arruinar la operativa de todo un año por esta circunstancia.
El ratio MEGAN de 0.5 es un buen valor. En realidad es la tasa de crecimiento del capital con este sistema. De forma que la exponencial de 0.5: exp(0,5)=1.65 es lo mismo que decir que operado activamente este sistema debería generar un 65% de ganancia anualizada. El detalle de este cálculo queda fuera del propósito de este artículo y para más información remitimos al lector al artículo original sobre el ratio de MEGAN, en inglés.
En esta simulación la única nota negativa es que tenemos un número pequeño de operaciones, 38. Con este número tan pequeño, aunque cumple el mínimo de 30 no es posible extraer conclusiones concluyentes sobre un sistema de trading. Más adelante probaremos diferentes parámetros y conseguiremos un número más adecuado de operaciones.
El sistema Gustafson tiene muchas características deseables pero quizás la mejor sea su simplicidad. Con solo 3 sencillas reglas hemos creado un sistema de trading bueno, con ratio de Sharpe superior a 1.
Optimización del sistema Gustafson
Es posible que desde que Gustafson diseñó este sistema el número de días de caída y de subida (los parámetros) hayan variado. A continuación vamos a optimizar estos parámetros para intentar mejorar en la medida de lo posible las buenas estadísticas que tenemos ya.
Una optimización exhaustiva, mirando todas las combinaciones de parámetros nos arroja los siguientes valores como óptimos:
- Número de días de caída: 3
- Número de días de subida: 2
- Número de días en las operaciones: 3
Cuando operamos con estos parámetros el resultado es:

Que como vemos es mucho mejor que el anterior. El ratio de Sharpe ahora es de 1.6, la ganancia es mucho mejor (114.000 dólares). Quizás a costa de ser un poco más rápido (lo que se ha traducido en una pequeña disminución en el Profit factor) pero al operar más nos genera 113 operaciones que es un número del cuál sí que podemos extraer conclusiones estadísticamente fiables.
A esta muestra de 113 operaciones le podemos hacer la prueba estadística y ver si el sistema tiene una ganancia promedio mayor que cero. Pero antes hay que darse cuenta de que el sistema, si fuera implementado en real no tendría límite en cuanto a lo que se pudiera perder en una operación. No hay stop loss. Si una compra va mal entonces si los siguientes 8 días fueran un desplome del mercado el sistema podría quebrar una cuenta por no tener límite en las pérdidas.
Vamos a añadir un stop loss.
Control del riesgo
El stop loss va a ser una distancia desde el punto de compra que sea un múltiplo del rango de variación diaria (ATR o Average True Range). Cuando probamos diferentes múltiplos del ATR encontramos que el mejor está a una distancia de 4 ATRs, de forma que no influye mucho (está lejos) y a la vez limita la máxima pérdida posible a 4 ATRs. Al hacer esto las estadísticas varían ligeramente pero ahora tenemos la confianza de que podemos operar este sistema con dinero real porque la máxima pérdida de una operación estará bajo control. Las nuevas estadísticas son:

Que como vemos no son muy diferentes de las anteriores. Probablemente la diferencia se deba a una o dos operaciones que tuvieron una pérdida mayor de 4 ATRs y que ahora están bajo control.
Prueba estadística del sistema Gustafson
Ahora vamos a hacerle dos pruebas. La primera va a ser comprobar la validez estadística de este sistema. La segunda (si pasamos la primera) será probarlo en datos que el sistema no ha visto nunca. Esto es lo que se llama la prueba fuera de muestra (Out of Sample) y que es imprescindible porque es equivalente a poner a funcionar un sistema con dinero real, ante unas operaciones futuras que no se sabe cómo van a ser.
Si ahora exportamos las operaciones y las pasamos a un software de gestión de capital como MSA (Market System Analyser) obtenemos las mismas estadísticas que acabamos de presentar (confirmando que la exportación se hizo correctamente) además de visualizar su curva de capital. Este programa nos va a permitir probar estadísticamente el sistema.

El riesgo de cada operación es exactamente de 4 rangos o ATRs. El software nos calcula la ganancia promedio en múltiplos del riesgo y la desviación. Los valores que arroja son:

Con estos datos podemos calcular el estadístico t, que es:


El mismo software nos hace la prueba estadística y la presenta así:

Donde vemos que la ganancia promedio de 1.023 dólares tiene una desviación de 887, así que en el peor de los casos tendremos una ganancia de 136 dólares. La probabilidad de que la ganancia promedio sea mayor que cero es del 96.98% así que supera el 95% de confianza que habíamos escogido como umbral de fiabilidad estadística.
Pues bien, ya tenemos un sistema que de forma científica demuestra que no es cierta la hipótesis nula de que su ganancia promedio sea cero. Esta es la forma correcta de hacer las cosas. Ahora bien, todo esto sale de una muestra limitada de operaciones, una secuencia fija que siempre se va a comportar de la misma manera. Si las operaciones tuvieran la misma distribución de ganancias y pérdidas, pero vinieran en otro orden entonces tendríamos diferentes curvas de capital. La simulación de Montecarlo nos ayudará a ver qué sucede cuando se juntan muchas pérdidas juntas, así podremos saber la probabilidad de que una de las curvas se vaya a cero.
Simulación de Montecarlo
Cada una de estas curvas representa una posible evolución del capital cuando operamos nuestro sistema. Hay que tener en cuenta que nunca podremos anticipar las operaciones futuras, así que conviene utilizar una aproximación estadística al trading.
Si hacemos un análisis de Montecarlo al sistema Gustafson obtenemos los siguientes resultados:

El software calcula 500 curvas de capital y de estas curvas el peor drawdown alcanzado es del 38%. Un valor muy bueno. El valor medio del drawdown de todas las curvas es del 8.59%, un valor excelente.
Como vemos podemos esperar unas 7 pérdidas seguidas. Y después de 30 operaciones la probabilidad de que perdamos la mitad del capital (50%) es nula. Sin embargo hay un 24.8% de probabilidades de que tengamos una ganancia del 50%.

Simulación fuera de muestra
Ahora vamos a probar el sistema en datos que no ha visto nunca. Para ello habíamos reservado los últimos 4 años, del 2008 al 2012. Siempre se debería escoger como datos fuera de muestra el periodo más reciente porque un sistema que se deteriore en los últimos años podría estar indicando que ya no funciona, que estaba basado en una ineficiencia del mercado que ya se ha corregido. Pues bien, cuando probamos el sistema Gustafson (3,2,3) en el periodo 2008-2012 el resultado es:

Que es un resultado impresionante para ser fuera de muestra. Con una ganancia de 95.000 dólares y un máximo drawdown del 20% estamos ante un sistema excelente, como demuestra su ratio de Sharpe de 2.1.
Y llegamos al final de esta serie de artículos. Ahora que tenemos un sistema que funciona y que hemos demostrado que efectivamente es así. Vamos a aplicarle Gestión de Capital para optimizar sus ganancias.

Gestión de Capital del sistema Gustafson
El modelo de gestión de capital que utilizaremos va a ser tan sencillo como arriesgar un porcentaje fijo del capital en cada operación. Puesto que el riesgo actual de cada operación es de 4 ATRs calcularemos el número de futuros a operar de lasiguiente manera:

De esta forma, al dividir el riesgo monetario entre el riesgo en puntos el resultado será el número de contratos a operar para que si la operación sale mal se pierda el porcentaje planificado de capital. Esta es una estrategia bien simple pero a la vez muy potente que permite un crecimiento geométrico del capital, ya que cuando tengamos ganancias acumuladas nos hará incrementar el tamaño de la posición.
Para saber cuál es el riesgo óptimo podemos pedirle al software que pruebe diferentes valores. Esto lo vemos en la figura 11. Hay un riesgo a partir del cual no se gana más por arriesgar más sino todo lo contrario. A partir del 50% de riesgo la ganancia cae hasta la total destrucción de la cuenta.

Es conveniente explicar aquí que no estamos considerando el drawdown. Evidentemente un riesgo tan excesivo como el 50% produce un drawdown del 72%. No hay diferencia entre que un sistema no funcione o que arroje un drawdown del 72% porque cuando uno está en una situación así no sabe si va a salir de ella.
El lector debe notar que la curva de beneficio/riesgo de la figura 11 se parece a la curva de campana de la teoría de f óptima (ver Vince “Portfolio Management Formulas”) pero se acelera a partir del riesgo óptimo. Esto es debido a que la aproximación de riesgo óptimo de Vince es determinista mientras que los resultados de un sistema de trading son aleatorios (dentro de unos parámetros estadísticos). Es decir, si calculamos suficientes curvas de capital entonces la que mayor ganancia dará será siempre aquella que está justo antes del colapso, porque será aquella en que se juntaron más ganancias y con el máximo riesgo.
Vamos a calcular ahora un riesgo óptimo en el sentido de que nos permita extraer el máximo beneficio de este sistema pero con un drawdown aceptable del 30% o menor. Cuando simulamos en MSA con esas características obtenemos un valor de riesgo de:
22%
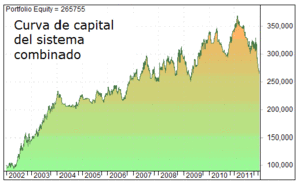
Si operamos el sistema Gustafson (3,2,3) durante el periodo de muestra 2000-2008, al 22% de riesgo por operación obtenemos los siguientes resultados:

Una ganancia de más de 300.000 dólares con un drawdown del 27%. Este es un resultado excelente que viene determinado por una gestión de capital adecuada.