Buenas tardes a tod@s,
Después de tratar en éste y algún otro blog de delta y algunas de las griegas de segundo orden que le afectan (gamma, color...), creo que llega el momento de hablar sobre vega.
Vega mide la sensibilidad de la opción respecto a su volatilidad implícita. Recuerdo que cada serie dentro de cada vencimiento tiene su propia volatilidad implícita. Matemáticamente es la derivada del valor de la opción con respecto a dicha volatilidad implícita.

Vega habitualmente se expresa como la variación en la prima de la opción por cada punto porcentual de variación en su volatilidad implícita.
Todas las opciones compradas tienen vega positiva y todas las opciones vendidas vega negativa.
Determinadas estrategias como los straddle sobre todo en vencimientos lejanos, son particularmente sensibles a la evolución de la volatilidad y vega sería un elemento de riesgo a controlar.
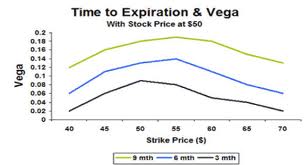
Vega presenta un mayor valor en las opciones a dinero, además es mayor cuanto más lejana sea la expiración. Por contra vega disminuirá cuanto más se meta en dinero o más se vaya a fuera de dinero la opción.
Es complicado mantener una posición en varios strikes y vencimientos vega neutral debido a los siguientes factores:
1. Los niveles de Vega son diferentes en cada strike y cambian de modo diferente en cada uno de ellos. Además la totalidad del volatility smile no se moverá de modo idéntico en los distintos vencimientos. De hecho los vencimientos alejados son los más sensibles a vega, mientras que los más cercanos son más sensibles a theta y a gamma.
2. La oferta y demanda de opciones ocasiona que algunos strikes coticen con mayor volatilidad implícita, mientras otros ven disminuir o permanecer inalterada dicha volatilidad implícita. El interés abierto influye muchas veces en esta mayor oferta y demanda de opciones.
VANNA
La vega de una opción no es constante. Vega cambia a medida que cambia el precio del subyacente y cambia la volatilidad, como mencionaba anteriormente. Vanna en una opción mide el cambio en vega originado por cambios en el precio del activo subyacente. Si los movimientos de precio y volatilidad se correlacionan positivamente el comprador de la opción con vanna positivo sacaría provecho a esta situación.
VOLATILIDAD ESTRUCTURA TEMPORAL (VOLATILITY SMILE)
La estructura temporal de la volatilidad es la curva que representa las diferentes volatilidades implícitas de las opciones con vencimientos diferentes. Tal curva surge en parte debido a que la volatilidad implícita en las opciones con vencimiento más cercano cambia mucho más rápido que la volatilidad implícita de las opciones con vencimiento más lejano. Sin embargo, la estructura temporal de la volatilidad también se presenta debido a la reversión a la media de la volatilidad. Además el efecto de los cambios en la volatilidad en el precio de la opción con vencimiento más cercano, en magnitud, es menor que en aquellas otras opciones con vencimiento más lejano. La mayoría de los creadores de mercado toman ventaja de las diferentes volatilidades para cubrir sus libros o para arbitrar diferentes anomalías percibidas en la volatilidad. Estas estrategias han de ponderarse por los diferentes efectos en vega.
En el siguiente enlace trataba sobre la estructura temporal de volatilidades y su evolución a lo largo del tiempo Volatility Smile y su Evolución a lo largo del Tiempo
VOMMA
Como mencionaba vega cambia a medida que cambia el precio del activo subyacente y cambia la volatilidad. Vomma en una opción se define como el cambio en vega debido a los cambios originados en la volatilidad. Vomma mide la convexidad del precio de una opción con respecto a la volatilidad. De algún modo vomma es a vega lo que gamma es a delta. Los tenedores de opciones con una vomma alta se benefician por tanto de un incremento en la volatilidad de la volatilidad.
Si algún lector es aficionado a Matlab incluyo una función para calcular la prima, la delta y la vega de una call y una put con strike E en Matlab
function [C, Cdelta, Cvega, P, Pdelta, Pvega] = ch10(S,E,r,sigma,tau)
%
% Input arguments: S = asset price at time t
% E = exercise price
% r = interest rate
% sigma = volatility
% tau = time to expiry (T-t)
%
% Output arguments: C = call value, Cdelta = delta value of call
% Cvega = vega value of call
% P = Put value, Pdelta = delta value of put
% Pvega = vega value of put
%
% function [C, Cdelta, Cvega, P, Pdelta, Pvega] = ch10(S,E,r,sigma,tau)
if tau > 0
d1 = (log(S/E) + (r + 0.5*sigmaˆ2)*(tau))/(sigma*sqrt(tau));
d2 = d1 - sigma*sqrt(tau);
N1 = 0.5*(1+erf(d1/sqrt(2)));
N2 = 0.5*(1+erf(d2/sqrt(2)));
C = S*N1-E*exp(-r*(tau))*N2;
Cdelta = N1;
Cvega = S*sqrt(tau)*exp(-0.5*d1ˆ2)/sqrt(2*pi);
P = C + E*exp(-r*tau) - S;
Pdelta = Cdelta - 1;
Pvega = Cvega;
else
C = max(S-E,0);
Cdelta = 0.5*(sign(S-E) + 1);
Cvega = 0;
P = max(E-S,0);
Pdelta = Cdelta - 1;
Pvega = 0;
end
Añado finalmente unos gráficos que muestran la relación entre vega-precio del activo subyacente, vega-tiempo a vencimiento y vega-volatilidad implícita


Finalmente una gráfica que muestra en una call binaria su variación por vega ante cambios en la volatilidad implícita. Las distintas griegas, si bien en opciones binarias tienen menor importancia que en las opciones vanilla, son un elemento de medición de riesgos que sería importante que los distintos intermediarios facilitaran en sus plataformas.

Saludos
