Me gustaría comenzar este artículo explicando brevemente la base en la que se fundamenta una de las asignaturas base del Máster en Finanzas que estoy cursando actualmente, Applied Portfolio Management (Gestión de Carteras Aplicada). En esta asignatura nos enseñan la manera de invertir buscando la combinación de activos financieros que maximicen en binomio rentabilidad-riesgo, asumiendo que el riesgo es igual a la volatilidad de las acciones. Este estilo de inversión está basado en la teoría moderna de carteras, de la que ya he hablado alguna vez en este blog.
La mayor parte del contenido de esta asignatura no me parece compatible con la gestión de carteras mediante Value Investing, aunque creo que una parte de la asignatura puede resultar útil en algunos casos y bajo ciertas condiciones. Me refiero al coeficiente de correlación.
¿Qué mide el Coeficiente de Correlación?
En la Wikipedia podemos encontrar esta buena explicación de lo que es la correlación: “La correlación es la medida de asociación entre variables. En probabilidad y estadística, la correlación indica la fuerza y la dirección de una relación lineal entre dos variables aleatorias. Se considera que dos variables cuantitativas están correlacionadas cuando los valores de una de ellas varían sistemáticamente con respecto a los valores homónimos de la otra: si tenemos dos variables (A y B) existe correlación si al aumentar los valores de A lo hacen también los de B y viceversa.”
El coeficiente de correlación sirve para medir la correlación entre 2 variables. La ventaja que tiene este coeficiente sobre otras herramientas para medir la correlación, como puede ser la covarianza, es que los resultados del coeficiente de correlación están acotados entre -1 y +1. Esta característica nos permite comparar diferentes correlaciones de una manera más estandarizada.
El coeficiente de correlación se puede calcular con Excel mediante el comando “COEF.DE.CORREL”. También se puede calcular mediante la fórmula:
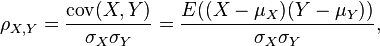
Siendo Cov (X,Y) la covarianza entre las series temporales X e Y, y σX e σY las desviaciones estándar de X e Y.
Interpretación
Como he mencionado antes, el coeficiente de correlación tiene un valor acotado entre -1 y +1. Los valores cercanos a cero indican que no hay asociación entre las variables. Valores cercanos a uno indican una asociación fuerte, mientras que los valores cercanos a menos uno indican una asociación fuerte pero inversa.
Por ejemplo, si el coeficiente de correlación entre dos activos financieros es mayor que 0,70, podemos decir que están muy correlacionados positivamente. Por el contrario, si el valor de este coeficiente está entre -0,20 y +0,20, la correlación será baja. Por último, si el coeficiente de correlación es menor que -0,70 existirá una gran correlación, pero negativa.
¿Puede ser útil en el Value Investing?
En mi opinión, creo que el uso del coeficiente de correlación puede resultar útil en el Value Investing en algunos casos. Este coeficiente nos puede ayudar a la hora de optimizar la diversificación de nuestra cartera si escogemos acciones con un coeficiente de correlación bajo. Esta afirmación puede ser muy discutible, por lo que debemos mirar los problemas del coeficiente de correlación como guía a la hora de diversificar en el Value Investing.
A la hora de usar el coeficiente de correlación, primero hemos de tener en cuenta que este coeficiente mide la correlación entre retornos, es decir, la diferencia en precios, pero no en valor. Así que debemos examinar las causas de la correlación para hacer un uso más adecuado de este coeficiente. Otro factor a tener en cuenta es que este coeficiente está basado en los datos del pasado. Por lo tanto hay que tener en consideración que el coeficiente de correlación puede variar a lo largo del tiempo.
Una solución a estos problemas es tener en cuenta las causas de la correlación. Para ello, puede resultar útil analizar los modelos de negocio y analizar si tiene sentido o no el valor de este coeficiente. En otras palabras, este coeficiente nos puede servir de guía, pero sin ser su resultado definitivo a la hora de escoger las empresas de nuestra cartera de inversiones. Esto se debe a que si diversificamos invirtiendo en empresas de distintos sectores, podremos evitar problemas si en el futuro hay una crisis en un sector específico, en este caso el bancario, como está ocurriendo en la actualidad.
En conclusión, el coeficiente de correlación puede resultar útil a la hora de buscar valores o sectores en los que podamos mejorar nuestra diversificación. Eso sí, siempre hay que analizar la lógica detrás del valor del coeficiente y analizar si su valor se adecúa a las características de la empresa que hay detrás que esa cifra.


