La semana pasada hablábamos sobre la volatilidad realizada, afirmando que la volatilidad no mide la dirección que ha tenido el mercado, ni si un activo se ha movido al alza o a la baja. Mide sólo la dispersión de su movimiento. Se puede equiparar, por lo tanto, la desviación típica de los movimientos del activo.
Decíamos también que normalmente, especialmente de cara a los modelos de valoración de opciones, etc se asume la hipótesis de que el mercado eficiente. y por tanto la distribución de la variación de los precios debería seguir aproximadamente una distribución normal.
Sin embargo, la realidad, que siempre supera la ficción, nos demuestra que la distribución del rendimiento de la mayoría de activos que cotizan en los mercados financieros no es normal. Y es aquí donde entran los siguientes momentos de la distribución: la asimetría y la curtosis.
Para definir una distribución de frecuencias a través de números, podemos utilizar diferentes estadísticos estadísticos básicos. Los más conocidos: media y desviación típica. El primero nos da una medida de más o menos donde está el peso de la distribución y el segundo de si este peso se distribuye de forma concentrada o no.
Si una distribución fuera un bolígrafo que queremos sujetar con la yema del dedo, la media sería el punto donde debemos sujetarlo. La desviación típica sería el margen que tendría para poder hacerlo.
Cuando calculamos las rentabilidades que un activo podría tener en el futuro, lógicamente estamos obligados a ver lo que hizo en el pasado (seguramente no haga lo mismo, pero al menos "rimará"). En este sentido, por ejemplo, cuando analizamos, por ejemplo, un fondo de inversión, buscaremos cuál ha sido su rentabilidad en el pasado. Por otro lado, será interesante ver también cuál es su desviación típica, puesto que es una manera de medir el riesgo. Si comparamos entre dos activos querremos elegir aquel que por cada unidad de riesgo tomada nos de una mayor rentabilidad. De ahí la utilidad de ratios como el de Sharpe.
Ahora bien, que la volatilidad sea una forma de medir el riesgo no significa que sea la forma de medir el riesgo. Ni siquiera que sea la mejor forma.
Por ejemplo, sería interesante tener en cuenta la
curtosis de la distribución, que se refiere al tamaño de las patas de la distribución. Cuanto mayor sea la curtosis, mayor la concentración de datos cerca de la media de la distribución coexistiendo al mismo tiempo con una relativamente elevada frecuencia de datos muy alejados de la misma.
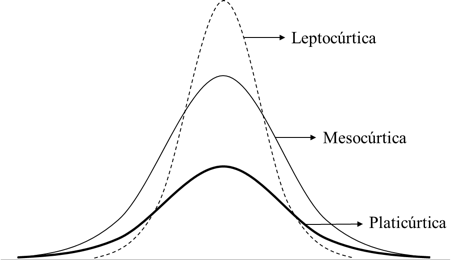
En imágenes:
El nombre viene del griego kurtos, que significa "arqueado" o "abultado". En castellano también se nombra a veces como apuntamiento o coeficiente de apuntamiento. Una distribución normal es mesocúrtica. Cualquier distribución con curtosis diferente a la normal se dice que tiene "exceso de curtosis".
Respecto a la asimetría, una distribución asimétrica, como indica su nombre, es aquella en la que existen resultados en las colas de la distribución, lo que provoca que una de las patas sea más larga que la otra.
Distribuciones de activos
Un distribución normal es simétrica (no tiene asimetría positiva ni negativa) y mesocúrtica. Si encontramos una distribución de retornos de un activo o de una estrategia que sea leptocúrtica sabremos que, a diferencia de una normal, habrá más resultados que sean cercanos a la media y algunos resultados más extremos. Si la distribución tiene asimetría negativa, entonces sabremos que, frente a la normal, habrá resultados negativos muy extremos.
Una estrategia de inversión basada en la venta de opciones fuera de dinero, por ejemplo, sin más filtros, podría ser una estrategia con fuerte asimetría negativa: normalmente se van pagando primas estables, por lo que la mayoría de retornos se concentran en torno a la media, pero de repente un movimiento de mercado podría provocar una fuerte pérdida.
Veamos algunas distribuciones de retorno de los principales activos. Por ejemplo, la renta variable. Como vemos en la siguiente imagen, la distribución de la renta variable es más apuntada de lo normal (leptocúrtica) y con una importante asimetría negativa (más resultados en el extremo negativo de lo que sugiere una normal):
Otras distribuciones muestran características similares, por ejemplo los bonos. En las siguientes imágenes se puede ver un índice agregado de Renta Fija en USD. Su distribución es más apuntada que una normal y tiene simetría negativa. A ka derecha, la distribución de retornos de un índice de Renta Fija Emergente, con mayor curtosis (muy apuntada) y con fuerte simetría negativa. Tiene lógica: existen episodios de riesgo y de tensión en los países emergentes, normalmente contagiados por el incremento de la incertidumbre en una zona.
Finalmente, la distribución del oro. También con algo de asimetría negativa y con apenas curtosis.
Estrategias y Asset Allocation
Como hemos visto, raras veces una distrubición de retornos de los activos que componen la cartera sigue una distribución normal. Por lo tanto, curtosis y asimetría son dos conceptos esencial de gestión de riesgo.
La forma tradicional de diversificar es encontrar activos lo más descorrelacionados para reducir riesgo sin impactar en la rentabilidad. Pero sabiendo que las distribuciones de activos y de la mayoría de estrategias de inversión no sigue una normal, lo que trataremos de buscar a la hora de construir y diversificar una cartera y tratar mitigar el riesgo no es sólo centrarnos en su ecuación Rentabilidad / Riesgo.
Por tanto, puede haber combinaciones de activos que no reduzcan directamente la desviación típica, pero sí que impacten fuertemente sobre la curtosis o la asimetría. Lo ideal es encontrar la distribución con mayor rentabilidad esperada, menor desviación típica (riesgo), mayor asimetría positiva y, en este caso, mayor curtosis. La mayor curtosis no es buena en sí misma, sino en el caso de que haya asimetría positiva.
En este sentido, por ejemplo, el oro parece que aporta estabilidad a una cartera de Renta Variable y Renta Fija no sólo por su capacidad de diversificar su riesgo a través de la desviación típica, sino porque reduce su curtosis. Lo vimos en detalle
en este artículo.
El índice SKEW
Lo veremos más en detalle cuando expliquemos qué es el VIX. Pero vale la pena echar un vistazo al índice SKEW. Y de ahí el interés del índice SKEW. publicado por el CBOE.
Este desconocido índice, mide las perspectivas del mercado sobre la asimetría de los rendimientos futuros:
Grandes caídas de la renta variable como la del 87, por ejemplo, enseñaron diferentes cosas a los operadores. Entre ellas, que el logaritmo de los rendimientos no sigue una distribución normal. De hecho, los rendimientos bursátiles se caracterizan por su notable asimetría negativa.
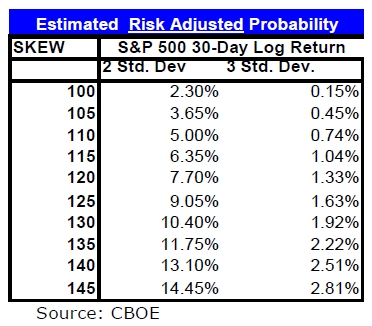
El riesgo de tener un resultado muy negativo (muy a la izquierda de la distribución) es lo que se conoce como el riesgo de cola (el riesgo de que salga un valor atípico, por ejemplo dos o más desviaciones estándar por debajo de la media). En el S&P 500, este riesgo es significativamente mayor que en una distribución logarítmica normal. En este contexto, un índice SKEW que marcase 100, significaría que los operadores piensan que este riesgo es similar al de una distribución normal. Por encima de 100 , los operadores opinan que la probabilidad de un rendimiento atípico es más significativo. La media del indicador se sitúa en el entorno de 120.
Se piensa que la probabilidad estimada de un rendimiento atípico del S&P 500 es la siguiente de acuerdo al valor del índice SKEW:
En resumen: A la hora de estimar los riesgos al rendimiento futuro del s&p 500, podemos tener en cuenta el VIX como la volatilidad estimada por los operadores de mercado. Por su parte, el índice SKEW nos puede dar una idea del riesgo de cola. Lo veremos en detalle más adelante.