Vamos a comenzar una serie de artículos sobre la volatilidad, intentando utilizar en la medida de lo posible un lenguaje cercano y tratando de alcanzar todos los conceptos, pero sin intención de entrar en los detalles más técnicos. Trataremos los siguientes puntos (sujetos a cambios si parecen oportunos, iremos actualizando los links según los vayamos publicando):
- ¿Qué es la volatilidad?
- Volatilidad, curtosis y asimetría.
- ¿Es la volatilidad un riesgo?
- El impuesto de la volatilidad.
- La volatilidad implícita.
- Estructura Temporal, Smile, Skew y Superficie.
- La volatilidad futura.
- La volatilidad como clase de activo.
- Invertir en el VIX.
Ya hemos escrito otros artículos en el blog sobre volatilidad, así que aprovechamos para añadirlos a este índice y también para darles un repaso y hacer una redición (por ejemplo, al artículo de volatilidad y asimetría llevo tiempo con ganas de hacerle un cambio).
A ver si nos queda algo chulo como la serie que hicimos sobre psicología y aprovechamos para dejarlo bonito al final y junto en un documento .pdf. Por ahora, empecemos por el principio: ¿Qué es la volatilidad?
Significado.
Del latín, volatilis, que significa "equipado con alas", en finanzas la volatilidad es una medida de la variabilidad de los mercados financieros. Cuanto mayor sea la volatilidad de un activo, mayores los cambios en sus precios. La volatilidad mide por tanto la frecuencia e intensidad de los cambios en el precio de un activo, mostrando la estabilidad o inestabilidad del mismo.
De forma más visual, imagina que los precios tienen una dirección y una velocidad. La "dirección" puede ser alcista o bajista. La "velocidad" de estos movimientos, siguiendo este ejemplo, sería la volatilidad.
Es fundamental diferenciar entre "volatilidad realizada", "volatilidad implícita" y "volatilidad futura".
- La realizada es un indicador ex-post, esto es, mide la volatilidad observada en el mercado. Es una medida de la dispersión de los retornos de un activo en un periodo de tiempo, y se calcula como la desviación estándar de los retornos.
- La implícita en cambio es un indicador ex-ante, que refleja las expectativas respecto a la variabilidad de un activo. Normalmente se calcula a través del precio de las opciones financieras. La analizaremos en detalle en el próximo artículo.
- Finalmente, la volatilidad futura es la que no conocemos (y que cualquier operador de opciones desearía conocer). Todos los modelos de estimación de volatilidad intentan predecir este valor.
Hoy nos centraremos en la Volatilidad Realizada.
En general, en cualquier variable aleatoria, la volatilidad realizada se puede calcular como la varianza o la desviación típica. En mercados financieros, la volatilidad realizada se define como la desviación típica de una serie histórica de retornos en un activo para un periodo determinado de tiempo en el pasado y respecto a un intervalo de tiempo (por ejemplo diario, semanal, mensual, etc).
|
Fuente: http://probabilidad2013a.blogspot.com/2013/05/calculo-de-la-media-y-la-desviacion.html |
Independientemente del intervalo temporal con el que se calcule, la volatilidad se suele presentar anualizada, para poder compararla más fácilmente.
Anualizarla es sencillo, porque es proporcional a la raíz cuadrada del tiempo. Es decir, si la volatilidad es diaria, para anualizarla no hay más que multiplicarla por la raíz cuadrada del número de días de trading que hay en un año: 252. Si es mensual, por la raíz cuadrada de 12, etc.
Por ejemplo, para anualizar una volatilidad diaria del 1%: 1% x raíz(252) = 15.87%.
Medida de dispersión.
La volatilidad no mide la dirección del mercado, ni si un activo se mueve al alza o a la baja. Mide sólo la dispersión del movimiento.
Normalmente, especialmente de cara a los modelos de valoración de opciones, etc se asume la hipótesis de que el mercado eficiente. Si el mercado es eficiente, el movimiento de los precios se produce sólo cuando haya nueva información (si no hay nuevas noticias, los precios se mantendrán sin movimiento). Como esta información es desconocida y su aparición es aleatoria (no se sabe qué va a salir ni en qué momento exacto), los precios varían de forma aleatoria. Por tanto la distribución de la variación de los precios debería seguir aproximadamente una distribución normal.
Si la evolución de los precios siguieran una distribución normal, podríamos asegurar que sus valores se distribuirán de la forma siguiente:
- 68,3% estarán hasta a 1 desviación típica alejados de la media.
- 95,2% de los valores estarán a una distancia de 2 desviaciones sobre la media.
- 99,7% estarán a 3 desviaciones de la media.

Fuente: https://mathbitsnotebook.com/Algebra2/Statistics/STstandardNormalDistribution.html
En todo caso, de acuerdo a la desigualdad de Chebyshov, sabemos que independientemente de la forma de la distribución, el porcentaje de la valores que estará a k desviaciones respecto a la media es al menos de 1 - 1 / K^2. Se distribuirá por tanto de esta manera:
- Al menos 36% de las observaciones estarán a 1,5 veces la media.
- 75% a 2 desviaciones de la media.
- 94% a 4 desviaciones de la media.
Medida del riesgo.
Una volatilidad alta significa que el activo se mueve más que otro de volatilidad baja, pero no indica hacia dónde. Por ello muchos entienden que la volatilidad no es una buena medida del riesgo, porque incluye también el riesgo de resultados positivos y eso no puede ser considerado un riesgo.
A pesar de lo anterior, lo cierto es que las volatilidades altas suelen estar correlacionadas con rendimientos negativos. Esto puede parecer contradictorio con la teoría de que a mayor riesgo mayor potencial, pero los hechos demuestran que esa afirmación no tiene por qué cumplirse.
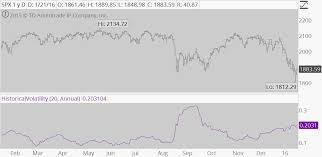
Así, por ejemplo, si medimos la evolución de la volatilidad a 20 días con el índice S&P 500, podemos ver como las caídas suelen coincidir con repuntes de la volatilidad.
En el mismo sentido, se conoce como la anomalía de la baja volatilidad ("low volatility anomaly") al hecho de que acciones con volatilidad realizada más baja obtienen mejor rendimiento a largo plazo que otras con volatilidad realizada superior.
Esta correlación negativa entre volatilidad y retornos se podría explicar en que las caídas de los mercados son más rápidas que las recuperaciones. Esto es, que los movimientos incitados por el miedo son más violentos que los que están basados en la confianza.
Por ello aunque la volatilidad no es una medida perfecta del riesgo, hace bastante buen trabajo, como veremos en el post referente a la volatilidad y el riesgo.
Con todo, esta correlación negativa ni es perfecta ni es similar todo el tiempo, a veces se reduce y en ocasiones se producen repuntes del mercado con aumentos de la volatilidad.
Así mismo, hay activos más volátiles que son más rentables a largo plazo, como la renta variable frente a los bonos. Sin embargo, lo importante no es sólo el resultado sino si estamos preparados psicológicamente y con educación financiera suficiente como para soportar los periodos en los que esta variabilidad vaya en nuestra contra.
A similar retorno, preferimos menor volatilidad.
Para terminar con la explicación de hoy, cuando el retorno es similar, lógicamente preferimos la que menos variabilidad presente en los retornos. De hecho, la volatilidad influye en los retornos finales: activos con un mismo retorno medio simple tienen un menor retorno compuesto si son más volátiles:
Aunque los 6 casos parezcan iguales al calcular la media simple, con el A tendremos un retorno superior que con el F y una menor volatilidad.
Es cierto que a veces con diferentes volatilidades tenemos en mismo retorno, compuesto, pero cabe preguntarse si ha valido pagar el precio psicológico de la mayor variabilidad del activo.
Lo explicamos con más detalle en próximos posts como: "El impuesto de la Volatilidad".