Continuamos con nuestra serie de artículos sobre la volatilidad, tratando hoy el tema del Smile, Skew y superficie de la volatilidad. Como recapitulación de los posts que ya hemos hecho y los que quedan, dejamos este índice.
- ¿Qué es la volatilidad?
- Volatilidad, curtosis y asimetría.
- ¿Es la volatilidad un riesgo?
- El impuesto de la volatilidad.
- La volatilidad implícita.
- Estructura Temporal, Smile, Skew y Superficie.
- La volatilidad futura.
- La volatilidad como clase de activo.
- Invertir en el VIX.

Decíamos en el post anterior que la volatilidad implícita se obtiene cambiando la incógnita de los modelos de valoración de opciones: en vez de calcular la prima de una opción, ponemos en la fórmula qué prima está cotizando ahora en el mercado y tratamos de calcular la volatilidad.
Uno de los problemas de esto es que cada opción de cada vencimiento tendrá una volatilidad implícita diferente. Para simplificar, se suele seleccionar la volatilidad de las opciones ATM (en el dinero) como "la cifra estándar" de volatilidad implícita.
Esto tiene sentido porque normalmente son las opciones más líquidas y las que suelen ser más sensibles a las variaciones de la volatilidad.
Skew
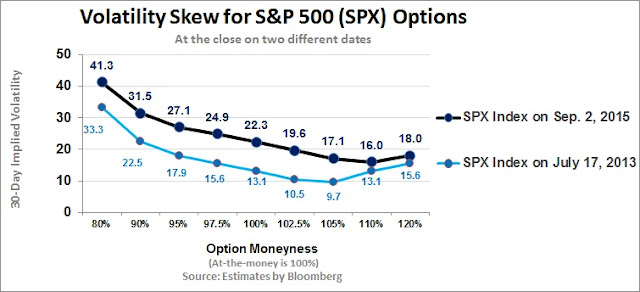
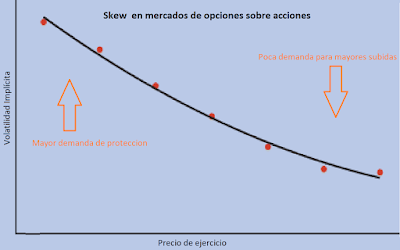
Con todo, se pueden graficar las diferentes volatilidades implícitas dependiendo del precio de ejercicio. En los mercados de renta variable, este dibujo de la relación entre volatilidad implícita (eje vertical) y precio de ejercicio (eje horizontal) suele adoptar una forma de "mueca", como una media sonrisa descendente, que se conoce como skew.
Se suele justificar esta forma típica de mueca con pendiente negativa en las protecciones de los inversores frente a grandes caídas del mercado a través de compras de PUT fuera de dinero (con precios de ejercicio -strikes- alejados del precio actual de las acciones y por lo tanto con primas asequibles). Si el precio de la acción cae de forma notable, el comprador de PUTS fuera de dinero se beneficiará, paliando en parte las caídas de su exposición a renta variable.
La relación es por lo tanto la consecuencia de una relación negativa entre la volatilidad implícita y el mercado subyacente. Además, las caídas fuertes (drawdowns) de los mercados de acciones suponen, en media, movimientos más intensos y violentos que las subidas, que suelen ser más espaciadas en el tiempo (y menos volátiles, por tanto, tal y como hablamos aquí).
En términos de volatilidad, que haya una mayor demanda de las opciones más alejadas del dinero permite que cotice relativamente más alta que la que está en el dinero y se forma por tanto es figura de mueca (es más caro comprar la volatilidad fuera de dinero que la que está en el dinero).
Los inversores de acciones están dispuestos a pagar más por una mayor protección contra las caídas de mercado que por una posible subida. Como los vendedores de protección asumen un mayor riesgo potencial, exigen un "volatility premium".
De lo anterior, se desprende que la relación entre volatilidad implícita y precio de ejercicio cambia. De hecho, no siempre muestra esa forma de mueca y la figura varía dependiendo del momento o de la clase de activo.
Por eso, la estructura de la volatilidad por precios de ejercicios nos puede dar información respecto al posicionamiento de los inversores. Si comparar la volatilidad implícita actual ATM frente a sus medias históricas nos indica las expectativas (el sentimiento) del mercado respecto a los precios actuales, la pendiente del skew nos indica las expectativas respecto al futuro. Normalmente, el skew se mide siguiendo el diferencial entre las put strike 90% (ATM = 100%) y las call 110%.
Una pendiente muy negativa respecto al pasado puede implicar que los inversores ven una mayor probabilidad de que el precio del subyacente caiga, por lo que estarán dispuestos a pagar un mayor precio por las protecciones (permitiendo que la volatilidad de los strikes OTM aumente relativamente más que la volatilidad ATM). Por otro lado, si la pendiente es plana, los inversores estarán mostrando una mayor complacencia.
Aunque sea un fenómeno raro en acciones, podría ser que la curva incluso se invirtiera totalmente y tomase pendiente positiva, mostrando una complacencia extrema, puesto que una forma así indicando unos inversores dando mayor probabilidad a nuevas subidas fuertes que a una caída de magnitud. Esta forma de la curva suele ser más común en materias primas, especialmente cuando los inversores esperan un fuerte déficit de oferta.
Smile
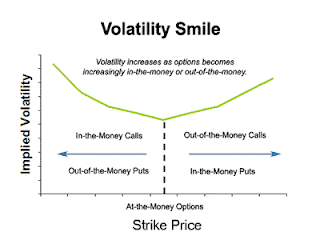
Otra forma común de esta relación entre volatilidad implícita y strikes se conoce como smile (sonrisa) de volatilidad.
Esta forma se suele relacionar con el exceso de curtosis en las distribuciones de rentabilidad del activo subyacente. El exceso de curtosis supone que las observaciones extremas sean más probables que una distribución normal (por tanto, más probable de lo asumido por los modelos tradicionales de cálculo de la prima de las opciones). Esto hace que el valor de las opciones muy ITM (en el dinero) y muy OTM (fuera de dinero) sea superior al de las opciones ATM, creando por lo tanto esta sonrisa.
Esta forma de smile es especialmente común en las opciones sobre divisas, debido a la demanda de coberturas tanto frente a una fuerte apreciación como frente a una fuerte depreciación (y en ambos lados de la ecuación, es decir, de unas divisas frente a otras).
Estructura Temporal
Del mismo modo que la volatilidad implícita cambia en relación al precio de ejercicio, también es diferente dependiendo del plazo. Se puede representar por tanto también las diferentes volatilidades implícitas para cada plazo. Esta curva se conoce como la estructura temporal de la volatilidad.
Esta curva, que también varía dependiendo de las expectativas, muestra qué piensan los operadores respecto a la volatilidad en el futuro.
Si los inversores estiman que el riesgo de corto plazo se incrementa notablemente (debido por ejemplo a un evento) la volatilidad de los periodos más cortos pueden repuntar fuertemente frente a la de los periodos más largos.
En el siguiente gráfico, (tomado prestado de este excelente y recomendable artículo de Funds People) se puede ver una estructura temporal de un índice de acciones en una situación de relativa tranquilidad de mercado:
Superficie de la volatilidad
Finalmente, se puede riza algo más el rizo combinando en un gráfico de tres dimensiones la estructura temporal y el skew.
Y ahora, empecemos a limpiar el polvo de nuestra bola de cristal y a sintonizar Cuarto Milenio, porque en el siguiente post hablaremos de volatilidad futura.