En el artículo de hoy, que es la tercera parte de la serie de artículos sobre Psicología en el trading resultado de transcribir mi presentación de Psicología de Mercados y Behavioral Finance en el Curso de Bolsa por Navidad que impartimos el pasado diciembre, hablaremos un poco de lo mal matemático que es Homer. Y ya os expliqué que Homer es nuestro asesor principal.
Puedes encontrar la primera parte en este link y la segunda en este otro.
Ya sabemos que la ley de números grandes permite que la probabilidad funcione: en dos lanzamientos de monedas podemos tener un 100% de caras, en un millón seguramente tengamos un 50% salvo que usemos una moneda trucada.
La ley de los números pequeños, unida a la ilusión de control y la búsqueda de patrones nos hace buscar orden en cosas que no lo tiene.
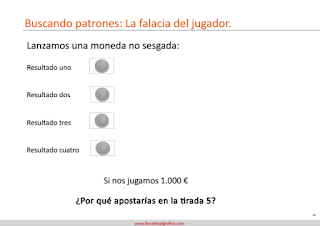
De esa tendencia de nuestra mente de buscar patrones que comentábamos el otro día, gracias al asesoramiento de Homer, nacen falacias como la siguiente: a priori, hay una baja probabilidad de lanzar una moneda no sesgada 8 veces y que resulte en 8 cruces. ¡Pero es la misma probabilidad exactamente, a priori, que la de sacar cualquier otro resultado!
Y además, cuando los eventos son independientes unos de otros, o dicho de otro modo, cuando el resultado anterior no influye en el próximo, la probabilidad se resetea en cada nuevo lanzamiento. Así, en la falacia del jugador o falacia del apostador de Montecarlo. Es decir, que si tiramos 4 veces una moneda y salen 4 caras seguidas, la probabilidad de sacar una quinta en el siguiente resultado es… pues del 50%.
En resumen, se nos da fatal la probabilidad.
Compliquemos un poco los acertijos, que los anteriores seguro que ya los conocíais (y Spock os ayudó un poco). En este será fácil perderse, pero no te preocupes. Sólo es para mostrar cómo efectivamente se nos da mal la probabilidad, especialmente dependiendo de cómo hagan la pregunta: ambas cosas básicas en los mercados financieros:
Imagina que lanzo dos monedas no sesgadas y te aseguro que “al menos una ha salido cara”. ¿Cuál es la probabilidad a priori de que el resultado hayan sido dos caras?
La respuesta más habitual es el 50%. Pero no. Al asegurar que uno de los dos lanzamientos ha salido cara eliminamos la oportunidad del resultado cruz-cruz. Queda por tanto cara-cara y cara-cruz por lo que, a priori, la probabilidad es de 1/3. Si hubiera dicho que el primer lanzamiento fue cara, entonces las probabilidades de una segunda cara sí serían del 50%.
Es un caso muy parecido al problema de Monty Hall, que tan mal resultado me dio explicar en un Bolsalia, y perdimos mucho tiempo en esta parte. Que no te importe tanto entenderlo bien como entender que las matemáticas son muchas veces contraintuitivas y que necesitamos a Spock para resolverlas.
Por si te interesa el tema de Monty Hall, adjunto un vídeo que lo explica bien (de la excelente película 21 Black Jack):
O este otro en el que lo explican más sencillo:
En fin, que somos unos matemáticos pésimos, y en esos contextos de aleatoriedad en los que nos jugamos los cuartos, más.
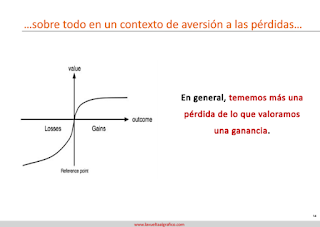
Daniel Kahneman, junto a su amigo Amos Tversky, de los que tanto hemos hablado en nuestro blog, desarrollaron en los 80 la prospect theory. Uno de los componentes más interesantes de esta teoría es la parte que define el dolor que causa una pérdida. La aversión a las pérdidas: a las personas nos duele más una pérdida de lo que nos alegra una ganancia similar. Esto es, nos hace más infeliz perder 100 € que feliz ganarlos.
Un estudio interesante sobre este tema es el que realizaron Benartzi y Thaler, publicado en 1995. En el mismo, se daba a cada participante 20 USD. Debían jugar 20 rondas a un juego en el que podían invertir o no 1 USD. Si decidían invertirlo, le daban el USD al investigador, que lo lanzaba al aire. Si salía cara, el sujeto perdía el USD. Si salía cruz, ganaba 2,5 USD. Si el sujeto decidía no invertir el USD, lo acumulaba y se pasaba a la siguiente ronda.
La mejor estrategia a priori para el juego anterior es, sin duda, invertir en todas las rondas. Si calculamos el valor esperado de jugar todas las rondas, sería: 50% x 2,5 + 50% x 0%. Es decir, en media ganaríamos 1,25 USD cada ronda y el valor estimado al final del juego es de 1,25 USD esperados x 20 rondas = 25 USD. Sólo hay una probabilidad entre 8 de terminar el juego con menos dinero del que empiezas. Sin embargo, en media, los participantes del juego finalizaron con 22,8 USD. Muchos de los sujetos preferían dejar de invertir después de una racha de pérdidas, a pesar de que los resultados fueran independientes unos de otros: la mala experiencia los volvía más conservadores evitando que pudieran recuperar más fácilmente lo perdido.
La peor consecuencia de la aversión a las pérdidas es el conocido como efecto disposición, que es lo que nos hace cortar rápido las ganancias pero dejar correr las pérdidas. Hay mucha literatura sobre el efecto disposición, pero sin duda la que más me ha llamado la atención es la relacionada con los monos capuchinos.
Keith Chen y Laurie Santos, de la Universidad de Yale, demostraron cómo de arraigado está el efecto disposición no ya en los humanos, sino en los primates.
La cosa es que la psicóloga Laurie Santos comenzó a trabajar con un grupo de monos capuchinos que habían sido educados para entender lo básico del intercambio de objetos. Keith Chen, amigo de Laurie y economista, se enteró de esto y propuso a la psicóloga educarles en el dinero y llevar a cabo una serie de experimentos de comportamiento. Así, enseñaron a los monos a cambiar pequeños discos plateados por comida. Vamos, a usar dinero. Podían comprar manzanas o uvas o gominolas con aquellos discos que recibían de los investigadores.
Entonces, probaron a aumentar o bajar los precios solicitados por las uvaso las gominolas, para probar las leyes de oferta y demanda, y los monos lo entendieron. Cuando “subía el precio” de las gominolas, consumían menos. Y viceversa.
Pero el experimento clave para lo que nos interesa consistió en que un investigador, cuando un mono le daba una moneda para comprar una uva, tiraba el disco al aire y si salía cara le daba dos uvas y si salía cruz, sólo una. Por otro lado, otro investigador, cuando los monos le daban la moneda para comprar una uva, les mostraba dos uvas. Luego tiraba la moneda al aire, si salía cara le daba las dos uvas y si salía cruz, guardaba una uva y le daba la otra.
En ambos casos, los capuchinos recibían el mismo número de uvas, en media. Pero el primer investigador las mostraba como una potencial ganancia y el segundo como una potencial pérdida. Pronto, los monos capuchinos comenzaron a elegir al investigador que no mostraba las dos uva. Es decir, que aunque el resultado fuera el mismo, el sufrimiento de perder una uva era mayor que la satisfacción de ganarla.
Si quieres saber más sobre estos experimentos, no te pierdas este vídeo de Laurie Santos.
Desde mi punto de vista, sólo a través de unas técnicas muy rigurosas de money management y de control de las posiciones, tanto ganadoras como perdedoras, el efecto puede atenuarse, pero nunca eliminarse del todo, ni siquiera en los inversores profesionales.
- La importancia de la Psicología en los mercados financieros (primera parte).
- La importancia de la Psicología en los mercados financieros (segunda parte).
- La importancia de la Psicología en los mercados financieros (tercera parte).
- La importancia de la Psicología en los mercados financieros (cuarta parte).
- La importancia de la Psicología en los mercados financieros (quinta parte).
- La importancia de la Psicología en los mercados financieros (sexta parte).
- La importancia de la Psicología en los mercados financieros (séptima parte).
- La importancia de la Psicología en los mercados financieros (octava parte).
- La importancia de la Psicología en los mercados financieros (novena parte).
- La importancia de la Psicología en los mercados financieros (décima y última parte).
Tomás García-Purriños, CAIA
@tomasgarcia_p