A pesar de vuestra timidez a la hora de hacer comentarios, vamos a seguir con la serie de artículos sobre psicología del trading resultado de transcribir mi presentación de Psicología de Mercados y Behavioral Finance en el Curso de Bolsa por Navidad del pasado diciembre. A día de hoy las casi 17.000 lecturas que han recibido los artículos creo que avalan que generan interés suficiente. Os recuerdo dónde podéis encontrar los artículos anteriores:
- La importancia de la Psicología en los mercados financieros (primera parte)
- La importancia de la Psicología en los mercados financieros (segunda parte)
- La importancia de la Psicología en los mercados financieros (tercera parte)
- La importancia de la Psicología en los mercados financieros (cuarta parte)

Decíamos el otro día que a Homer se le da fatal la probabilidad. Y bueno, en realidad, las matemáticas en general.
Recuerdo que cuando estaba en primero de BUP, en clase de matemáticas, nuestro profesor le preguntó a un compañero que llevaba toda la hora hablando (conmigo, por cierto) por el resultado de un ejercicio que se había mandado para casa el día anterior. Rápidamente, yo, que era un empollón aunque hacía todo lo posible por no parecerlo, se lo chivé. Mi compañero repitió mi susurro en voz alta y el profesor le preguntó que cómo había llegado a ese resultado. Mi amigo respondió rápidamente –por la cuenta de la vieja, maestro.- Nuestro profesor, sabiamente, sentenció –si esta asignatura se llamase cuentas de una vieja, te pondría un sobresaliente. Pero como se llama matemáticas, te pongo un negativo.
Y es que todos conocemos bien el peligro de la cuenta de la vieja.
Por ejemplo, si en una operación pierdo un -30%, aunque luego recupere un +30% no me quedo igual que antes. No funciona así.
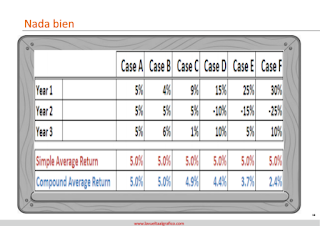
Lo anterior es sencillo de entender. Quizá algo menos intuitivo, pero fundamental, es el poder del interés compuesto. La forma de obtener los resultados de, por ejemplo, un fondo de inversión sí es importante. Las pérdidas influyen en el cálculo del rendimiento cuando se compone:
Por ejemplo, empezando con 100 € en el fondo A, terminamos con 115 €. Pero en el F, con 107,25 €. La rentabilidad media es similar, pero camino para llegar a ella influye a la hora de calcular la rentabilidad total.
Pero lo peor de todo este asunto es que mantenemos nuestros sesgos cuando juzgamos a los demás, como explicamos ampliamente aquí.
En un trabajo de Baron y Hersey, se pedía a un sujeto que eligiese entre obtener 200 USD con seguridad o arriesgarse y obtener 300 USD con una probabilidad del 80% o nada con un 20% de probabilidad. La esperanza matemática de arriesgarse es de 240 USD, muy superior a la de no arriesgar, y en principio la opción más lógica si fuéramos un robot. Pero cuando se elegía a otros sujetos, que tan sólo observaban el experimento, que valorase la elección como buena o mala, siento -30 la peor nota y +30 la mejor, ¡la valoración media cambiaba dependiendo del resultado! Es decir, en media la valoración era de +7,5 cuando se arriesgaba y ganaba y del -6,5 si se arriesgaba y perdía. Delirante.
Cómo valoramos la calidad de una elección depende por tanto del resultado y no del camino para llegar al mismo. En fin, que es como si alguien se hipoteca por 1 millón de euros, lo gasta en lotería y si le tocan dos asegurar que ha hecho lo correcto y felicitarle.
Pero lo verdaderamente divertido ocurre cuando juntamos todas estas malas decisiones de micro-behavioral finance y las agregamos en los mercados financieros. El resultado es sorprendente.
Porque lo lógico sería pensar que este mundo de sujetos tomando decisiones ineficientes, resultase en un mercado ilógico y absurdo. Pero lo cierto es que el mercado es bastante eficiente.
Y no lo digo yo, lo dice la gran mayoría de literatura teórica, que apoya bastante la hipótesis de la eficiencia de los mercados. Lo dice el hecho de que la gran mayoría de gestores son incapaces de batir al benchmark.
Es decir, el mercado refleja con bastante acierto las valoraciones. Esto es, que valor y precio suelen coincidir.
Y que conste, he dicho “bastante eficiente”, “con bastante acierto”, “suelen coincidir”… Porque aunque este no sea el post para discutir sobre si el mercado es eficiente, sí que adelantaré mi opinión personal (que conocéis de sobra si seguís este blog), el mercado es contradictorio. Es eficiente y no lo es.
O dicho de otra forma, es eficiente menos cuando no.
Pero no es el lugar para afrontar este interesante debate, y sí lo es para hablar de James Surowiecki, del que ya hemos hablado en este blog en otras ocasiones. Llamaba a esa eficiencia que surgía de opiniones ineficientes “la sabiduría de las masas”.
Bajo determinadas circunstancias, la combinación de información del grupo lleva a mejores resultados que los tomados por una sola persona, aunque sea experta en el tema. Surowiecki comentaba en su libro cómo un grupo de personas sin ningún conocimiento consigue hacer una mejor predicción del precio de un buey en una feria de ganado que los propios expertos. Pero lo que pretende decir se entiende mejor utilizando un estudio de Credit Suisse, en el que se analiza este efecto.
Al grupo de becarios del verano de 2013, se les pide que averiguaran el número de gominolas que había en una cesta. Se ofrecía un “incentivo” al que acertase (por ejemplo, quedarse con las gominolas, no lo recuerdo exactamente) y un “castigo” al que dijese el número más alejado (“castigo” dentro de lo razonable e incluso lo divertido del juego).
La estimación media de los 70 becarios que participaron era de 1427 y había ¡1416 gominolas en la cesta! Lo más interesante, ¡la desviación media de las estimaciones individuales era superior a 50!
De acuerdo a esta misma nota, hay tres requisitos que deben cumplirse para que las masas se hagan inteligentes:
- Diversidad de opiniones: por ejemplo, muchos participantes como los de un mercado de acciones.
- Un lugar donde las opiniones puedan agregarse: por ejemplo, el mercado de acciones.
- Incentivos. Es decir, premios para el que acierte, castigo para el que falle. No es necesario que el incentivo sea económico. Pero, por ejemplo, en el mercado de acciones, lo es.
Por todo lo anterior, es por lo que defiendo que los mercados son a la vez eficientes e irracionales.
¡Seguimos el próximo día!
- La importancia de la Psicología en los mercados financieros (primera parte).
- La importancia de la Psicología en los mercados financieros (segunda parte).
- La importancia de la Psicología en los mercados financieros (tercera parte).
- La importancia de la Psicología en los mercados financieros (cuarta parte).
- La importancia de la Psicología en los mercados financieros (quinta parte).
- La importancia de la Psicología en los mercados financieros (sexta parte).
- La importancia de la Psicología en los mercados financieros (séptima parte).
- La importancia de la Psicología en los mercados financieros (octava parte).
- La importancia de la Psicología en los mercados financieros (novena parte).
- La importancia de la Psicología en los mercados financieros (décima y última parte).
Tomás García-Purriños, CAIA
@tomasgarcia_p